はじめに
こんにちは。AI サービス開発部の千坂です。
主に AI Camera のクライアント側アプリの開発をしています。
AI Camera は、AI による画像解析技術を用いてカメラ画像を解析し様々な課題を解決するサービスです。
例えば、あらかじめ設定した進入禁止エリアに人が侵入したことを自動的に検出してアラートを上げる「侵入検出」機能を利用することで、監視カメラを人が常時監視する必要がなくなります。
アラートが発生した時点の状況を後から確認するために、カメラから取得した画像はストレージに保存します。
すべての画像を保存しているとストレージが不足してしまうため、保存した画像を削除する処理を定期的に行います。
本記事では、削除する画像を選択する処理を競技プログラミングの問題風に設計していきます。
課題
まずは、実装する機能の仕様を決めていきます。
アラートが発生した時点の状況を確認したいので、アラートが発生した時刻およびその前後の画像は削除対象にせず、それ以外の画像を削除対象とします。
ストレージは有限なので、十分に古い画像はアラートの有無に関わらず削除対象とします。
削除処理を行った直後にアラートが発生した場合にもその前後の画像が残っている必要があるため、十分に新しい画像はアラートの有無に関わらず削除対象にしません。
この仕様において削除対象とする範囲を表したのが以下の図です。
赤が削除対象とする範囲で、緑が削除対象としない範囲です。
削除対象とする赤の範囲を求めるのが今回の課題です。

問題の定式化
「古い」画像を削除することと「新しい」画像を削除しないことは明らかなので、その間で削除対象とする範囲を求めます。
その範囲を とします。
件のアラート情報があり、それぞれ時刻
の範囲を削除対象から除外することを表します。
どのアラートの範囲にも含まれない時刻の範囲をすべて求めてください、という問題になります。
解法1
削除対象の候補リストを で初期化し、そこから
を順次引いていくことを考えます。
、
,
と
を
とした場合を考えます。
まず、リストを で初期化します。
そこから最初のアラートの区間 を引くと、リストは
となります。
次の区間 を引くと、リストは
となります。
最後の区間 を引くと、リストは
となり、これが削除対象となる範囲です。
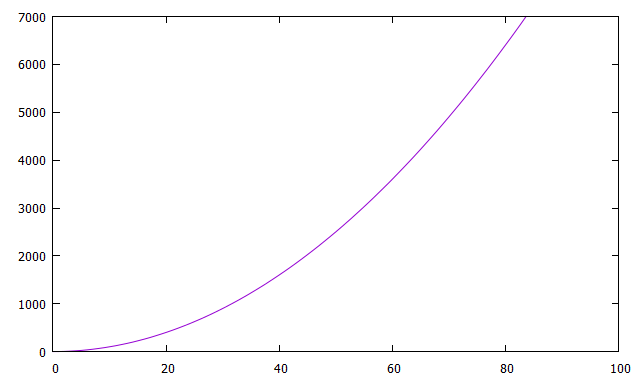
区間を1つ引くたびに候補リストの要素数は最大で1つ増えるため、計算量は となります。
※工夫すればこの方針でも計算量を落とせますが、別の方針を採用しました(解法2)。
解法2
では、以下のような方法ではどうでしょうか。
まず、 を昇順にソートします。
適当な変数 を用意し、
で初期化します。
ソートした列を走査して、それが区間の先頭 であれば
に
を加算し、終端
であれば
を減算します。
走査中、 の値が
となっている区間が求める区間となります。
解法1の場合と同様に、 、
,
と
を
とした場合を考えます。
をソートします。区間の先頭か終端かが分かるようにするために
または
を付けて書くと、
となります。
を
で初期化します。
ソートした列の最初が なので、その前の
の範囲は削除対象です。
で
となるため、
の範囲は削除対象ではありません。
で
となるため、
の範囲は削除対象です。
でそれぞれ
となるため、
の範囲は削除対象ではありません。
で
となるため、
の範囲は削除対象です。
以上から、削除対象は となり、解法1の結果と一致します。
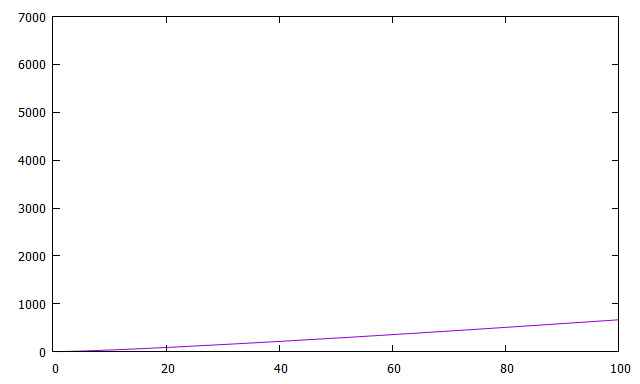
この方法では、ソートが 、その後の処理が
のため、全体の計算量は
となります。
解法1と比べて、データ量が多いときの計算時間がかなり短縮されることが分かります。
おわりに
競技プログラミングとしては簡単な問題になってしまいましたが、アルゴリズムを工夫することで計算時間を大幅に削減できることがお分かりいただけたでしょうか。
大きなデータを扱う際は、より適切なアルゴリズムがないか検討してみることをおすすめします。
オプティムでは一緒に働く仲間を募集しています。

