AlphaGoで学ぶ強化学習 ~次の一手を予測する将棋AIを作ってみよう~

こんにちは、R&Dの宮城です。

将棋の竜王戦が世間を賑わせる中、オプティムでも人知れず将棋AI vs 私の熱闘が繰り広げられていました。
今回の記事では強化学習について簡単に説明した後、次の一手を予測する将棋AIを作成し、作成した将棋AIと実際に戦ってみます。
※ 作成した将棋AIは強化学習ではなく教師あり学習で訓練されたものです。

強化学習の概要

強化学習は機械学習手法の一つです。

• 教師あり学習: 入力と入力に対する正しい出力(正解データ)が与えられ、出力が正解データに近づくように学習する
• 教師なし学習: 入力のみが与えられ正解データは与えられず、データのパターンなどを学習し分析する
• 強化学習: AI自身が与えられた環境下で試行を繰り返し、報酬が最大となるように学習する

文章の説明だけではわかりにくいと思いますので、強化学習を用いたAIモデルで最も有名と思われるAlpha Goを例に概要を説明させていただきます。
またディープラーニング系の将棋AIではdl-shogi が非常に有名です。AlphaGoは囲碁のAIなので将棋AIとは異なる箇所もあり、今回の記事作成にあたりdl-shogiは大変参考になりました。

Alpha Goは主に局面から次の一手を予測するPolicyNetwork、勝率を予測するValueNetworkの2つのネットワークで構成されています。

• PolicyNetwork: 13層の畳込みニューラルネットワーク。入力は局面の特徴量、出力は次の一手クラスを示す確率分布。
• ValueNetwork: 13層の畳込みニューラルネットワーク。入力は局面の特徴量、出力は局面の勝率。PolicyNetworkと異なり分類タスクではなく回帰。

各ネットワークは以下の手順で訓練されます。

• STEP1: 教師あり学習で次の一手を予測するPolicyNetworkを訓練する
• STEP2: STEP1で訓練したPolicyNetwork同士で決着がつくまで対戦し、勝敗を報酬としより勝ちやすい手を指すようPolicyNetworkを強化学習させる。同時に対戦結果からValueNetwork用の勝率教師データを作成する
• STEP3 PolicyNetwork同士の対局によって作成された勝率教師データを使用し、教師あり学習で勝率を予測するValueNetworkを訓練する

上記STEP2のように、報酬が大きくなるようにAI自身で学習するのが強化学習です。この場合勝利時の報酬 =1、敗北時の報酬 = -1と設定し、より勝ちやすい手を予測するように学習が進みます。教師データが不要のため膨大な数の試行によりネットワークを最適化できるというメリットがあります。

以上、強化学習を用いたAlpha Goの仕組みについて簡単に説明しました。
AlphaGoはPolicyNetworkとValueNetworkの結果を組み合わせて指し手を予測していますが、本記事ではSTEP1の「次の一手を予測するPolicyNetwork作成」までを試してみます。

将棋の補足説明

将棋の基本的な知識を簡単に補足しておきます。 将棋は下図のように 縦9マス x 横9マス の81マスの盤上で交互に駒を動かし敵の王様を打倒するというゲームです。

また、

• 敵陣に到達した駒は成る(進化する)ことができる
• 奪った敵の駒を自分の駒(持ち駒)として使用することができる

というルールもあります。特にこの持ち駒ルールによって指し手のバリエーションが爆発的に増加し、将棋AIの予測を困難にしています。

次の一手を予測するPolicyNetwork作成

入力特徴量

まずは指し手予測PolicyNetworkの入力となる特徴量を設計します。 dl-shogi、AlphaGoの特徴量を参考に以下の必要最小限の特徴を使用しました。

1. 駒の位置
2. 持ち駒の有無

駒の位置を表す特徴

駒の位置は各駒ごとに9x9のマス上に駒が存在すれば1, 存在しなければ0とします。以下は歩の位置の特徴を変換した例です。

駒の位置の特徴量は9x9の二値画像が全14駒分必要です。

持ち駒の有無を表す特徴

次に持ち駒の有無を表す特徴ですが、駒の位置の特徴に合わせこちらも9x9サイズとします。 こちらは単純に対象の駒を持っていれば9x9マス全てが1、持っていなければ全て0になります。
そして持ち駒の駒数ごとに9x9の特徴量を1つずつ用意します。持ち駒の特徴量は持ち得る最大の駒数分だけ用意するため、
'歩': 18枚、'香': 4枚、'桂': 4枚、'銀': 4枚、'金': 4枚、'角': 2枚、'飛': 2枚 の合計38枚分必要です。
例えば「歩」を1枚持っていた場合、下図のように所持している1枚目の歩の特徴量は全て1、2~18枚目の歩の特徴量は持ち駒にないため全て0となります。

入力特徴量まとめ

また、1. 駒の位置、2. 持ち駒の有無は先手、後手の2通り必要です。最終的な入力特徴量をまとめると以下の通りです。

• 先手の駒の位置: 14
• 後手の駒の位置: 14
• 先手の持ち駒: 38
• 後手の持ち駒: 38
• 合計 104

よって9 x 9 の2値画像、104 チャンネル分が次の一手を予測するPolicyNetworkへの入力となります。

出力クラス

次にネットワークの出力について考えます。次の一手を予測するとは言い換えると、どの駒がどの位置に移動するか(持ち駒から打たれる場合も含む)を予測するということです。
将棋の駒は成り駒を含めると '歩'、'香'、'桂'、'銀'、'金'、'角'、'飛'、'玉'、'と'、'成香'、'成桂'、'成銀'、'馬'、'龍'の14種類です。
よって 出力が14駒 × 9マス x 9マス = 1,134 クラスあれば全駒、全マスを網羅することができます。
これで次の一手予測問題を1,134クラス分類タスクに落とし込むことができました。
実際の出力は1,134通りの指し手ラベルであり、各ラベルが「３六歩」や「６八銀」のようなそれぞれの指し手に対応しています。

PolicyNetwork実装

PolicyNetworkの構造はAlphaGoと同じく13層のシンプルな畳み込みニューラルネットワークとし、カーネルサイズやフィルター等のパラメータはdl-shogiを参考に以下の通り実装しました。

【PyTorchでのPolicyNetwork実装】

import torch.nn as nn
import torch.nn.functional as F

class PolicyNetwork(nn.Module):
    def __init__(self):
        super().__init__()
        self.conv1 = nn.Conv2d(in_channels = 104, out_channels = 256, kernel_size = 3, padding = 1)
        self.conv2 = nn.Conv2d(in_channels = 256, out_channels = 256, kernel_size = 3, padding = 1)
        self.conv3 = nn.Conv2d(in_channels = 256, out_channels = 256, kernel_size = 3, padding = 1)
        self.conv4 = nn.Conv2d(in_channels = 256, out_channels = 256, kernel_size = 3, padding = 1)
        self.conv5 = nn.Conv2d(in_channels = 256, out_channels = 256, kernel_size = 3, padding = 1)
        self.conv6 = nn.Conv2d(in_channels = 256, out_channels = 256, kernel_size = 3, padding = 1)
        self.conv7 = nn.Conv2d(in_channels = 256, out_channels = 256, kernel_size = 3, padding = 1)
        self.conv8 = nn.Conv2d(in_channels = 256, out_channels = 256, kernel_size = 3, padding = 1)
        self.conv9 = nn.Conv2d(in_channels = 256, out_channels = 256, kernel_size = 3, padding = 1)
        self.conv10 = nn.Conv2d(in_channels = 256, out_channels = 256, kernel_size = 3, padding = 1)
        self.conv11 = nn.Conv2d(in_channels = 256, out_channels = 256, kernel_size = 3, padding = 1)
        self.conv12 = nn.Conv2d(in_channels = 256, out_channels = 256, kernel_size = 3, padding = 1)
        self.conv13 = nn.Conv2d(in_channels = 256, out_channels = 14, kernel_size = 1, padding = 1)
        self.fc1 = nn.Linear(14 * 11 * 11, 14 * 9 * 9)

    def forward(self,x):
        x = F.relu(self.conv1(x))
        x = F.relu(self.conv2(x))
        x = F.relu(self.conv3(x))
        x = F.relu(self.conv4(x))
        x = F.relu(self.conv5(x))
        x = F.relu(self.conv6(x))
        x = F.relu(self.conv7(x))
        x = F.relu(self.conv8(x))
        x = F.relu(self.conv9(x))
        x = F.relu(self.conv10(x))
        x = F.relu(self.conv11(x))
        x = F.relu(self.conv12(x))
        x = F.relu(self.conv13(x))
        x = x.view(x.size()[0], -1)
        x = self.fc1(x)
        return x

【PolicyNetwork表示結果】

PolicyNetwork(
  (conv1): Conv2d(104, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv2): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv3): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv4): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv5): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv6): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv7): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv8): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv9): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv10): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv11): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv12): Conv2d(256, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
  (conv13): Conv2d(256, 14, kernel_size=(1, 1), stride=(1, 1), padding=(1, 1))
  (fc1): Linear(in_features=1694, out_features=1134, bias=True)
)

上記PolicyNetworkの構造を確認してみると、畳み込みニューラルネットワークでよく使用されているプーリング層が存在しないことがわかります。
プーリング層では画像の領域ごとの情報をまとめて圧縮する処理が行われ、物体の位置ずれに頑強になります。
しかし、将棋や囲碁では駒が1マスずれただけで状況が一変してしまうので、位置情報は正確である必要があり、プーリング層なしで畳み込みニューラルネットワークをつなぎ合わせた構造としています。

PolicyNetwork訓練

ネットで公開されているAI vs AI の棋譜を使って訓練します。棋譜とは以下のように何手目に何を指したかなど対局開始から終了までの情報がすべてまとめられたものです。
この棋譜から入力に必要な特徴量を抽出してPolicyNetworkの訓練に使用します。

V2.2
N+宮城 自称7級
N-optim-shogi ？段
$EVENT:オプティム杯
$SITE:オプティム東京オフィス
$START_TIME:2021/09/27 19:05:00
$END_TIME:2021/09/27 20:21:00
P1-KY-KE-GI-KI-OU-KI-GI-KE-KY
P2 * -HI *  *  *  *  * -KA * 
P3-FU-FU-FU-FU-FU-FU-FU-FU-FU
P4 *  *  *  *  *  *  *  *  * 
P5 *  *  *  *  *  *  *  *  * 
P6 *  *  *  *  *  *  *  *  * 
P7+FU+FU+FU+FU+FU+FU+FU+FU+FU
P8 * +KA *  *  *  *  * +HI * 
P9+KY+KE+GI+KI+OU+KI+GI+KE+KY
+
+2726FU
-8384FU
・・・
・・・

以下の通り訓練データとテストデータを用意しました。

• 訓練データ: 74,461局、8,648,338手分
• テストデータ: 5,680局、727,226手分

訓練データが膨大なので3エポックだけ学習させ、訓練済みモデルのテストデータに対する精度は Accuracy=0.382 でした。
次の一手を約38%の確率で予測できているということですが、ランダムに予測すると約0.09%(1,134 分の1)の確率なのでまずまずの精度でしょうか。
これで次の一手を予測する将棋AIが作成できました！これを optim-shogi と呼ぶことにします。

実戦

それでは作成した将棋AI、optim-shogiくんと戦ってみましょう。
私の棋力は駒の動かし方を知っている程度ですが、「龍が如く」の将棋ミニゲームでアマ8級を名乗る敵を倒したことがあります。
以下、勝負の様子をダイジェストでお楽しみください。
(私が先手で下側の陣地、optim-shogiが後手で上側の陣地)

【1手目 (私の手番)】
私の先手番で対局開始です。まずは定石通り飛車先の歩をつきます。

【2手目 (optim-shogiの手番)】
optim-shogi も同じく飛車先の歩をついてきました。定石通りに指せているようです

【32手目 (optim-shogiの手番)】
私の不用意な桂馬ジャンプを３六歩打でしっかり咎めてきました。持ち駒も問題なく使えているようです。
しかも敵の王様はちゃっかり安全なところまで移動していますね。あれ、強いかも...

【60手目 (optim-shogiの手番)】
なんと敵陣深くに打ち込んだ私の飛車が捕獲されてしまいました。
しかも敵には最強の駒、龍を作られておりピンチです。

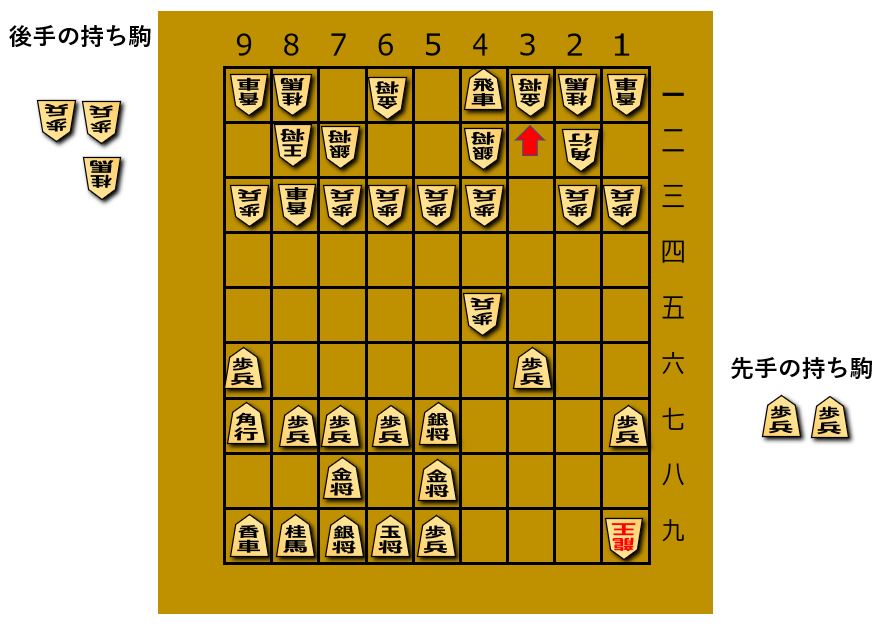
【78手目 (optim-shogiの手番)】
ここでoptim-shogiが反則手を指してしまいました。
第一候補は５七歩打だったのですが、これは同じ列に歩を２枚使用してしまう「二歩」という反則です。
optim-shogiの出力はルールに則した手かどうか考慮されていないのでこのように反則手を指してしまうことがあります。むしろ78手目まで合法手を指し続けたのはなかなかすごいですね。
仕方がないのでここは代わりに第二候補の６八銀打という手を採用してあげることにします。

【94手目 (optim-shogiの手番)】
反則を見逃してあげた恩を忘れ、2枚の龍で猛烈に攻め立ててきます。もしかするともう詰んでいるかもしれません。

【106手目 (optim-shogiの手番)】
必死に逃げたものの optim-shogiの8八金打ちにて、ついに玉の逃げ場がなくなり詰まされてしまいました。

この戦いの棋譜は以下の通りです。

V2.2
N+宮城 自称7級
N-optim-shogi ？段
$EVENT:オプティム杯
$SITE:オプティム東京オフィス
$START_TIME:2021/09/27 19:05:00
$END_TIME:2021/09/27 20:21:00
P1-KY-KE-GI-KI-OU-KI-GI-KE-KY
P2 * -HI *  *  *  *  * -KA * 
P3-FU-FU-FU-FU-FU-FU-FU-FU-FU
P4 *  *  *  *  *  *  *  *  * 
P5 *  *  *  *  *  *  *  *  * 
P6 *  *  *  *  *  *  *  *  * 
P7+FU+FU+FU+FU+FU+FU+FU+FU+FU
P8 * +KA *  *  *  *  * +HI * 
P9+KY+KE+GI+KI+OU+KI+GI+KE+KY
+
+2726FU
-8384FU
+2625FU
-8485FU
+6978KI
-4132KI
+3938GI
-8586FU
+8786FU
-8286HI
+0087FU
-8684HI
+3736FU
-3334FU
+9796FU
-7172GI
+3837GI
-5162OU
+3746GI
-6271OU
+2524FU
-2324FU
+2824HI
-7182OU
+2937KE
-0023FU
+2429HI
-3142GI
+3635FU
-3435FU
+4635GI
-0036FU
+3745KE
-3637TO
+0038FU
-3747TO
+5968OU
-8454HI
+2927HI
-0037FU
+3837FU
-4757TO
+6869OU
-5455HI
+3546GI
-5554HI
+3736FU
-4344FU
+2757HI
-5457HI
+4657GI
-4445FU
+4958KI
-0029HI
+0059FU
-2919RY
+8897KA
-0083KY
+0041HI
-3231KI
+4131HI
-4231GI
+9753UM
-0052FU
+5354UM
-0049HI
+6968OU
-0046KE
+5746GI
-4946RY
+0044KE
-1949RY
+4432NK
-3132GI
+5432UM
-0056KE
+6869OU
-0068GI
+7968GI
-5668NK
+7868KI
-2244KA
+3221UM
-0088FU
+6979OU
-8889TO
+7989OU
-0088GI
+8988OU
-0076KE
+2176UM
-4676RY
+8879OU
-7687RY
+0088GI
-8788RY
+7969OU
-8868RY
+5868KI
-0047KA
+0058GI
-0079GI
+6979OU
-4959RY
+0069KE
-0088KI
%TSUMI

結果

optim-shogi vs 私の熱戦は106手で私の敗北となりました。一度も王手をかけられないまま完膚なきまでに叩きのめされましたが、optim-shogiくんは78手目に２歩の反則をかましているので勝負に勝って試合に負けたといったところでしょうか。
少ない入力特徴量、かつシンプルな構造のネットワークでも初心者なら倒せるくらいの将棋AIを作成できることが確認できました。

今後の改善点としては出力クラスの修正があります。 現在の14駒 × 9マス x 9マス = 1,134クラスでは同じ位置に移動できる同種類の駒が複数ある場合に指し手を一通りに特定できません。指された駒がどこから来たか分かるような情報を追加し出力クラス数を修正する必要がありそうです。
また、今回は次の一手を予測するPolicyNetworkを作成したのみですので、AI同士で訓練する強化学習やValueNetworkを組み合わせることでさらに強力になると思われます。　

おわりに

オプティムでは時代の一手先を見通すエンジニアを募集しています。

ライセンス表記

記事内の将棋盤画像はdigipotさまの素材を使用させていただきました。
また、盤面の表示はmurosanさまの shogi-boardを使用させていただきました。
ありがとうございました。