こんにちは、プラットフォーム事業部の河内です。最近は新オフィスを堪能しています。
さて、今年の 3 月に NVIDIA から Instant NeRF という手法が発表されました。
NeRF がどんなものなのか、Instant NeRF が今までの手法と比べ何がすごいのかについては上記の記事でおおまかに掴めるかと思いますが、中身が気になるところです。
NVIDIA の記事中で Tiny CUDA Neural Networks ライブラリを使用とあるのでリポジトリを見てみると、どうやら TensorFlow や PyTorch を利用したものではなく、Instant NeRF の根幹となる手法のためにチューニングされたフレームワークのようです。
リポジトリの README では 2 つの手法とその論文が引用されており、ひとつは "fully fused" multi-layer perceptron、もうひとつは multiresolution hash encoding *1 です。今回は後者の multiresolution hash encoding を試してみます。
目次:
- Multiresolution Hash Encoding の概要
- Multiresolution Hash Encoding を PyTorch で実装してみる
- Multiresolution Hash Encoding で欠損した画像を復元してみる
- Multiresolution Hash Encoding の特徴ベクトルを可視化してみる
- おわりに
- 付録: 学習用のコード
Multiresolution Hash Encoding の概要
NeRF は位置ベクトルを入力として、MLP により色と密度を出力する手法です。ただし MLP では位置ベクトル (低周波な信号) から色と密度 (はるかに高周波な信号) への変換を学習することが難しいため、Positional Encoding と呼ばれる方法で位置ベクトルをより高次元かつ高周波なベクトルに変換します。Multiresolution Hash Encoding も Positional Encoding の役割を担う手法で、類似の手法と比べいくつか優れている点があります:
- 今までの手法よりも並列化しやすく、はるかに高速に動作
- 汎用性が高く、複数のタスクで優秀な成績
(Multiresolution Hash Encoding の論文 *1 では Positional Encoding という単語は出てきませんが、本記事中ではオリジナルの NeRF *2 の Positional Encoding と同等の役割の手法をまとめて Positional Encoding と表現します。)
さて、Multiresolution Hash Encoding の仕組みを見てみます。論文中の図解 (図1) がわかりやすいです。
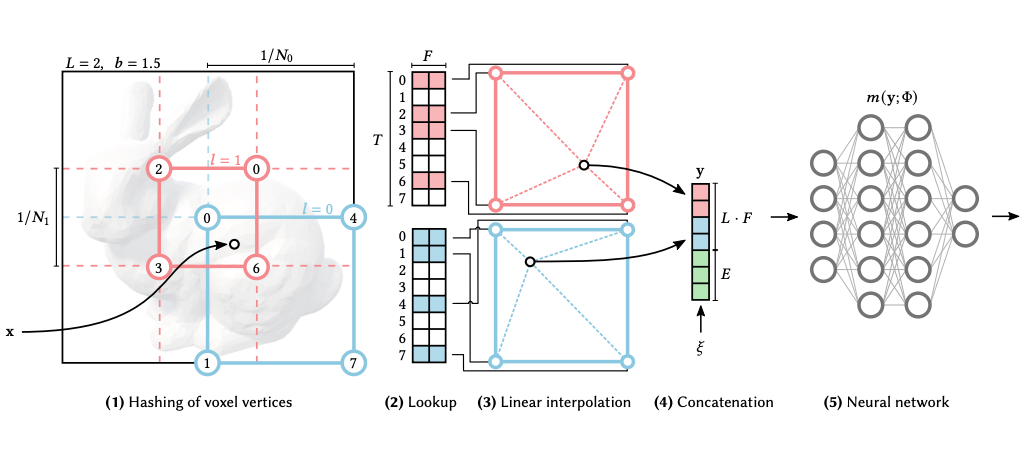
図にならい、位置から特徴ベクトルを計算する過程を簡単に説明してみます:
- 複数解像度 (ある解像度のことをレベルと表記、レベル数
) のグリッドに対し、位置
周辺のグリッド座標 (整数) をハッシュ関数により特徴ベクトルのインデックス (mod
) に変換する。つまり、あるレベルについて 2 次元座標であれば 4 点、3 次元座標であれば 8 点のインデックスが得られる。このインデックスは決定的に定まる
- 1 で得られたインデックスを使い、ハッシュテーブル内の特徴ベクトル (
次元) をルックアップする。この特徴ベクトルは MLP と一緒に学習する
- レベルごとに、2 で得られた周囲の特徴ベクトルから
の特徴ベクトルを線形補完する
- 3 で得られたレベルごとの特徴ベクトルを結合し、最終的な特徴ベクトルを作る。位置によらない情報 (視線方向など) も補助入力としてここで結合する
- 4 を MLP に入力
ハッシュテーブルは の要素をもち、各要素は
次元なので、学習可能なパラメータ数は
です。
が推奨されており、実質的には単一のハイパラメータ
で品質と計算コストのバランスを調整できます。
Multiresolution Hash Encoding を PyTorch で実装してみる
Multiresolution Hash Encoding のアプリケーションは NeRF を含め公開されていますが (instant-ngp)、今回はイメージを掴むために 2 次元画像を学習するモデルを PyTorch で実装してみます。モデルの概要を図1に示します。
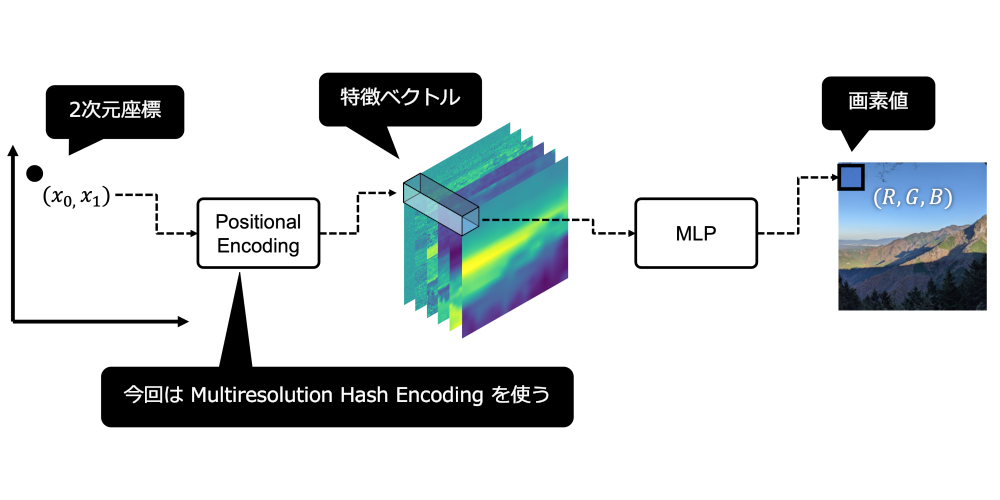
👨💻 実装
まずは入力を用意します。画素が位置ベクトルとなるような tensor としました。
import torch def make_position_vectors(width, height): xs = torch.linspace(0, 1, steps=width) ys = torch.linspace(0, 1, steps=height) x, y = torch.meshgrid(xs, ys, indexing='xy') return torch.stack([x, y])
次に、2 次元位置ベクトルをより高次元に埋め込むための Positional Encoding を用意します。今回は Multiresolution Hash Encoding を使います。実装からもわかりますが、学習可能なパラメータが含まれています。(私は最初、ハッシュテーブルの要素が定数だと誤解していました。)
import math from torch import nn from torch.nn import functional as F class MultiresolutionHashEncoder2d(nn.Module): def __init__(self, l=16, t=2**14, f=2, n_min=16, n_max=512, interpolation='bilinear'): super().__init__() self.l = l self.t = t self.f = f self.interpolation = interpolation b = math.exp((math.log(n_max) - math.log(n_min)) / (l - 1)) self.ns = [int(n_min * (b ** i)) for i in range(l)] # Prime Numbers from https://github.com/NVlabs/tiny-cuda-nn/blob/ee585fa47e99de4c26f6ae88be7bcb82b9295310/include/tiny-cuda-nn/encodings/grid.h self.register_buffer('primes', torch.tensor([1, 2654435761])) self.hash_table = nn.Parameter( torch.rand([l, t, f], requires_grad=True) * 2e-4 - 1e-4) @property def encoded_vector_size(self): return self.l * self.f def forward(self, x): b, c, h, w = x.size() def make_grid(x, n): g = F.max_pool2d(x * n, (h // n, w // n)).to(dtype=torch.long) g = g * self.primes.view([2, 1, 1]) g = (g[:,0] ^ g[:,1]) % self.t return g grids = [make_grid(x, n) for n in self.ns] features = [self.hash_table[i, g].permute(0, 3, 1, 2) for i, g in enumerate(grids)] feature_map = torch.hstack([ F.interpolate(f, (h, w), mode=self.interpolation) for f in features ]) return feature_map
そして、Encoder と MLP を含む全体のモデルを用意します。様々な Positional Encoding が試せるようにコンストラクタで Encoder を受けとるようにしています。
class Model(nn.Module): def __init__(self, encoder, num_planes=64, num_layers=2): super().__init__() self.enc = encoder # 1x1 convolution is equivalent to MLP for a point in the 2D-coordinates layers = [nn.Conv2d(encoder.encoded_vector_size, num_planes, 1)] for _ in range(num_layers - 2): layers += [nn.ReLU(), nn.Conv2d(num_planes, num_planes, 1)] layers += [nn.ReLU(), nn.Conv2d(num_planes, 3, 1), nn.Sigmoid()] self.mlp = nn.Sequential(*layers) def forward(self, x): feature = self.enc(x) out = self.mlp(feature) return out
⚗️ 実験
教師画像を読み込み、実装したモデルを学習します。train 関数は付録に記載しています。
from torchvision.io import read_image, ImageReadMode img = read_image('yama.png', ImageReadMode.RGB) img = img / 255 model = Model(encoder=MultiresolutionHashEncoder2d()) train('hash', img, model)
パラメータは論文を参考に、 としました。教師画像の解像度は
です。
学習の結果は以下のようになりました。右側の図は学習の 1 イテレーションごとの出力結果をアニメーションにしたものです。

細部まで再現できており、非常に良好な結果です。可視化のためにスロー再生のようになっていますが、実時間ではもっと高速に収束しています。オリジナルの NeRF *2 の Positional Encoding とも比較してみましたが、収束の早さ品質ともに Multiresolution Hash Encoding のほうが優れているようでした。
Multiresolution Hash Encoding で欠損した画像を復元してみる
前の実験ではすべての位置の画素値が観測できていることを前提としていましたが、現実ではそうもいきません。2次元画像ではあまり想像できませんが、NeRF 等ではすべての位置を網羅できていなくとも、ある程度欠損領域を補完することが求められます。あえて欠損させたスカスカの画像を作り、Multiresolution Hash Encoding の補完能力を確認してみます。
⚗️ 実験
マスク画像を作り、非マスク領域については学習しないようにします。train 関数のコードは付録に記載しています。
mask = torch.rand([512, 512]) < 0.1 model = Model(encoder=MultiresolutionHashEncoder2d()) train('hash_mask', img, model, mask=mask)
パラメータと入力画像については前回の実験と同様です。結果は以下のようになりました。

1 割程度の領域しか観測できていない状況ですが、そこそこ違和感なく補完できています。論文中でも述べられていますが、 Multiresolution Hash Encoding の特徴マップは連続なため、欠損領域についても補完することができます。今回は bilinear でグリッド上の特徴ベクトルを補完しましたが、よりパラメータを絞った状態で bicubic 等の補完方法を試してみても面白いかもしれません。
Multiresolution Hash Encoding の特徴ベクトルを可視化してみる
🔍 PCA による可視化結果
Multiresolution Hash Encoding が出力する特徴ベクトルがどのようなものであるか確認するために、グリッドのレベルごとの特徴ベクトル可視化してみます。可視化の方法は
- あるレベルの特徴ベクトル (今回は
なので 2 次元) を全画素について PCA にかけ、1 次元に削減
- 1 で得られたグレースケールの画像にカラーマップを適用し着色
としました。
可視化結果は以下のようになりました。今回は としたので、16 レベルごとの結果を示します。
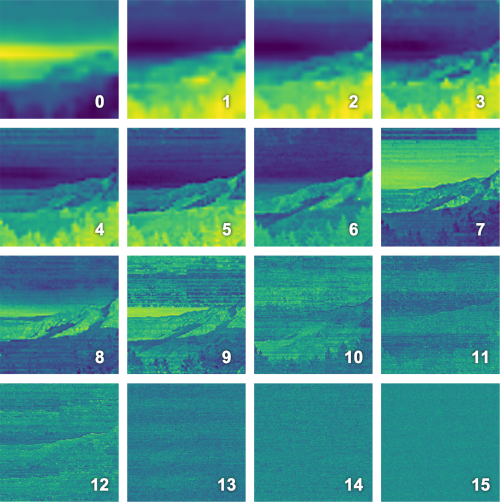
グリッドの解像度が異なるため当然かもしれませんが、低いレベルでは大域的な、高いレベルでは局所的な特徴を学習していることを確認できます。個人的に興味深いのは高いレベル (= 細かいグリッド) の可視化結果です。ハッシュ関数の性質なのか、ある種のフィルタのように機能しているように見えます。ただし、それが良い結果をもたらすのかどうかはわかりません。
おわりに
Multiresolution Hash Encoding を実際に実装し可視化してみることで、Instant NeRF の具体的な挙動がイメージできました。
まだ幅広く調査できているわけではありませんが、 NeRF 周辺は非常に面白いので今後も注目していきたいと思います。他の Neural Rendering 関係の手法も試してみたいですね。
オプティムではエンジニアを募集しています。ご興味があればぜひ。
付録: 学習用のコード
本文中で利用していた train 関数を記載します。
クリックで展開
from pathlib import Path from os import makedirs def save_image(x, name): p = Path(name).parents[0] if not p.is_dir(): makedirs(p) img = (x * 255).to(torch.uint8) write_png(img, name + '.png') def train(name, img, model, mask=None, steps=300, output_visualize=True): _, h, w = img.size() x = make_position_vectors(w, h) loss_fn = nn.MSELoss() optimizer = torch.optim.Adam([ { 'params': model.enc.parameters() }, { 'params': model.mlp.parameters(), 'weight_decay': 1e-6 } ], lr=0.01, betas=(0.9, 0.99), eps=1e-15) model.to(device) model.train() x, y = x.to(device), img.to(device) x = x.unsqueeze(0) y = y.unsqueeze(0) if mask is not None: mask = mask.to(device) for i in range(steps): pred = model(x) if mask is None: loss = loss_fn(pred, y) else: loss = loss_fn(pred * mask, y * mask) optimizer.zero_grad() loss.backward() optimizer.step() if output_visualize: save_image(pred[0].cpu(), f"outputs/{name}/{i:010d}")
*1:Müller, T., Evans, A., Schied, C., & Keller, A. (2022). Instant Neural Graphics Primitives with a Multiresolution Hash Encoding. ArXiv:2201.05989.
*2:Mildenhall, B., Srinivasan, P. P., Tancik, M., Barron, J. T., Ramamoorthi, R., & Ng, R. (2020). NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis. ECCV.

