PG BATTLE 2020 に参加しました

こんにちは。AI サービス開発部の千坂です。

2020/10/24 (土) に開催された PG BATTLE 2020 企業の部に参加しましたので、その時の感想や問題の紹介をします。

PG BATTLE とは
問題の紹介と感想
まとめ

PG BATTLE とは

PG BATTLE は「企業・学校対抗プログラミングバトル」で、問題として与えられる仕様を満たすプログラムを制限時間内に提出する形式の、いわゆる競技プログラミングのコンテストです。

問題は、例えば以下のようなものです。

$N$ 個の物があり、 $i$ 番目の物の汚さは $A_i$ です。
アライグマは物をキレイに洗うのが趣味です。アライグマが物を $1$ 秒間洗うと、洗った物の汚さが $1$ 減少します。
アライグマは同時に $2$ つ以上のものを洗うことはできません。
$N$ 個の物すべての汚さを $K$ 以下にするまでに必要な最小の秒数を求めてください。

制約：

$1 \le N \le 200,000$

$0 \le K \le 100,000$

$0 \le A_i \le 100,000$

入力中のすべての値は整数である。

https://products.sint.co.jp/hubfs/resource/topsic/pgb/2-1.pdf

これに対して、例えば以下のようなプログラムを回答として提出します（C 言語による回答例）。

#include<stdio.h>
#define max(p,q)((p)>(q)?(p):(q))
int main(){
    int n,k;
    long long ans=0;
    scanf("%d%d",&n,&k);
    for(int i=0;i<n;i++){
        int t;
        scanf("%d",&t);
        ans+=max(0,t-k);
    }
    printf("%lld¥n",ans);
}

https://products.sint.co.jp/hubfs/resource/topsic/pgb/code.pdf

回答を提出すると、制限時間の終了後に正解・不正解が自動的に判定され、正解であれば問題ごとに決められた点数が与えられます。
出力が誤っている場合のほか、プログラムの処理時間が既定値（2秒）を超える場合も不正解となります。

PG BATTLE は3人1チームで参加し、3人それぞれに異なる4問の問題セットが与えられます。
制限時間は4問で90分です。

問題の紹介と感想

オプティムからは千坂、今枝、西牟禮の3名でエントリーしました。
それぞれの担当した問題について、考察や感想を交えながら紹介します。

考察の内容については正しさを保証するものではありません。
問題の全文や正答例、解説動画については PG BATTLE 2020 の公式ページをご覧ください。

ましゅまろ

（担当：西牟禮）

一番柔らかい難易度の「ましゅまろ」を担当した、
サービス開発統括本部ソリューション開発部新卒の西牟禮です。
最近はWebRTCに関することに携わらせてもらっています。

1問目動物園 (Zoo)

人数 $X$ 未満の場合の1人あたりの入園料 $A$ と、
$X$ 以上の場合の1人あたりの入園料 $B$ 、入園者数 $N$ が与えられます。
$N$ 人の入園料の合計を求める問題です。
掛け算するだけですね。

2問目平均気温 (Average Temperature)

2地点の $A$ , $B$ の気温を $N$ 日間観測したとき、
どちらのほうが $N$ 日間の平均気温が高いですか？という問題です。
足し算するだけですね。

3問目距離感 (Sense of Distance)

2人組が $N$ 組いて、ペア1からペア $N$ まで番号がつけれられています。
これら $2N$ 人を一列に並べました。前から $i$ 番目の人はペア $A_i$ に属しています。
次の問題を $K=0,1,...,2N-2$ のそれぞれの場合について解いてください。
- 問題：ペアを構成する2人の間に存在する人の数が $K$ 人以下であるようなペアはいくつあるか?
- $1 \leq N \leq 10^ 5$
- $1\leq A_i \leq N$
- $A_i$ には1からNがちょうど2回ずつ現れる。

ペアの出現位置を記録してその差分を配列に持たせるような実装にしていました。
見直してみると、2重のfor文で $\mathcal{O}(10^{10})$ の計算をしていることに気づきました。
その部分を修正して無事通ったのでほっとしました。

4問目辞書順最小最短経路 (Minimum Lexicographical Shortest Path)

あるところに洞窟があります。
洞窟には $N$ 個の部屋と $M$ 本の通路があり、部屋には $1$ から $N$ の、通路には $1$ から $M$ の番号がついています。通路 $i$ を使うと、部屋 $A_i$ から部屋 $B_i$ へ移動することができます(逆方向の移動はできません)。同じ部屋同士を結ぶ通路が複数ある場合や、同じ部屋に戻ってくる通路がある場合もあります。
部屋 $1$ から部屋 $N$ への経路であって、通過する部屋の数が最小になるようなもののうち、部屋番号の列が辞書順最小となるものを求めてください。
- $2 \leq N \leq 10^ 5$
- $0 \leq M \leq 10^ 5$
- $1 \leq A_i, B_i \leq N$

この問題は解けなかったので、正しい解法は公式の解説をご覧ください！

所感

いつものコンテストとは異なり再提出ができないとのことだったので、しっかりと見直しをしました。
そのおかげで(?)キリ番を踏め、順位を伸ばせました。

せんべい

（担当：今枝）

真ん中の難易度の「せんべい」を担当した、20年度新卒の今枝です。
最近は、AICameraのフロントエンド(Vue.js) のお手伝いをしています。
今回、1問目から順に問題の感想を書いていきます。

1問目腕立て伏せ (Push Up)

問題の状態AC, WA, -が N 問分入力として与えられます。
(N問 - ACの状態の問題) * 5 を出力する問題です。
簡単なので、すぐ解けて一安心です。

2問目 5ベキ (Power of 5)

整数 N が与えられます。 $\frac{1}{5^ n}$ を正確に求めてください。

$1 \leq N \leq 60$

N は整数

末尾に余分な 0(trailing zero) をつけてはならない。

分数の問題ですね。

print(1/(5**n))

をしたいですが、末尾の0をつけてはいけなかったり、正しく値を求めなければいけません。
別のコンテストサイト(yukicoder)の問題で苦い思い出があるので、いったん3問目を見て、後から解きました。
3問目がとき終わってから実装しましたが、筆算と同じようにするだけでした。
賢いやり方は、 $\frac{1}{5^ n} = \frac{2^ n}{10^ n}$ に変換する方法です。実装が簡単になってすごいですね....

3問目左手法 (Left-Hand Rule)

H * W マスの迷路をスタートSからゴールQまで左手法探索したときの行動回数を出力問題です。(ただし、到達不可能な場合は代わりに-1を出力します。)

$1 \leq H \leq 1000$
$1 \leq W \leq 1000$

左手法の行動：

今いるマスの進行方向左側が道なら、90 度左に向きを変えてから、進行方向に 1 マス進む

そうではなく、今いるマスの進行方向正面が道なら、進行方向に 1 マス進む

そうではなく、今いるマスの進行方向右側が道なら、90 度右に向きを変えてから、進行方向に 1 マス進む

そうではなく、今いるマスの進行方向後側が道なら、180 度向きを変えてから、進行方向に 1 マス進む

いずれでもないなら何もしない

コツとしては、迷路の周りを壁で囲んであげると実装が少し楽になります。
到達不能な判定は、 $2HW$ 回移動した時点でゴールできていない場合に $-1$ を出力しました。
この問題を落としたらまずいので、何度も見直しをしました。

4問目ドミノ (Domino)

縦 H マス、横 W マスのグリッドがあります。これらのマスに 1×2 の大きさのタイルを置きます。タイルは、縦または横に連続する 2 つの空マスの上に置くことができます。
タイルを盤面からはみ出すように置くことや、他のタイルがすでに置かれているマスにタイルを重ねることはできません。
グリッドの全てのマスを覆うようなタイルの置き方は何通りありますか？
mod( $10^ 9 + 7$ ) で求めてください。

$1 \leq H \leq 5$

$1 \leq W \leq 10^ 4$

制約と問題からbitDP で解けそうですが、状態の持ち方がパッと分からなかったので、3問目の見直しをしてこの問題は諦めました。
プログラミングコンテストチャレンジブック (通称、蟻本) に実装がそのまま乗っていたらしいので、蟻本の読み込みが足りませんでした。

所感

ということで、3問解けて60点でした。

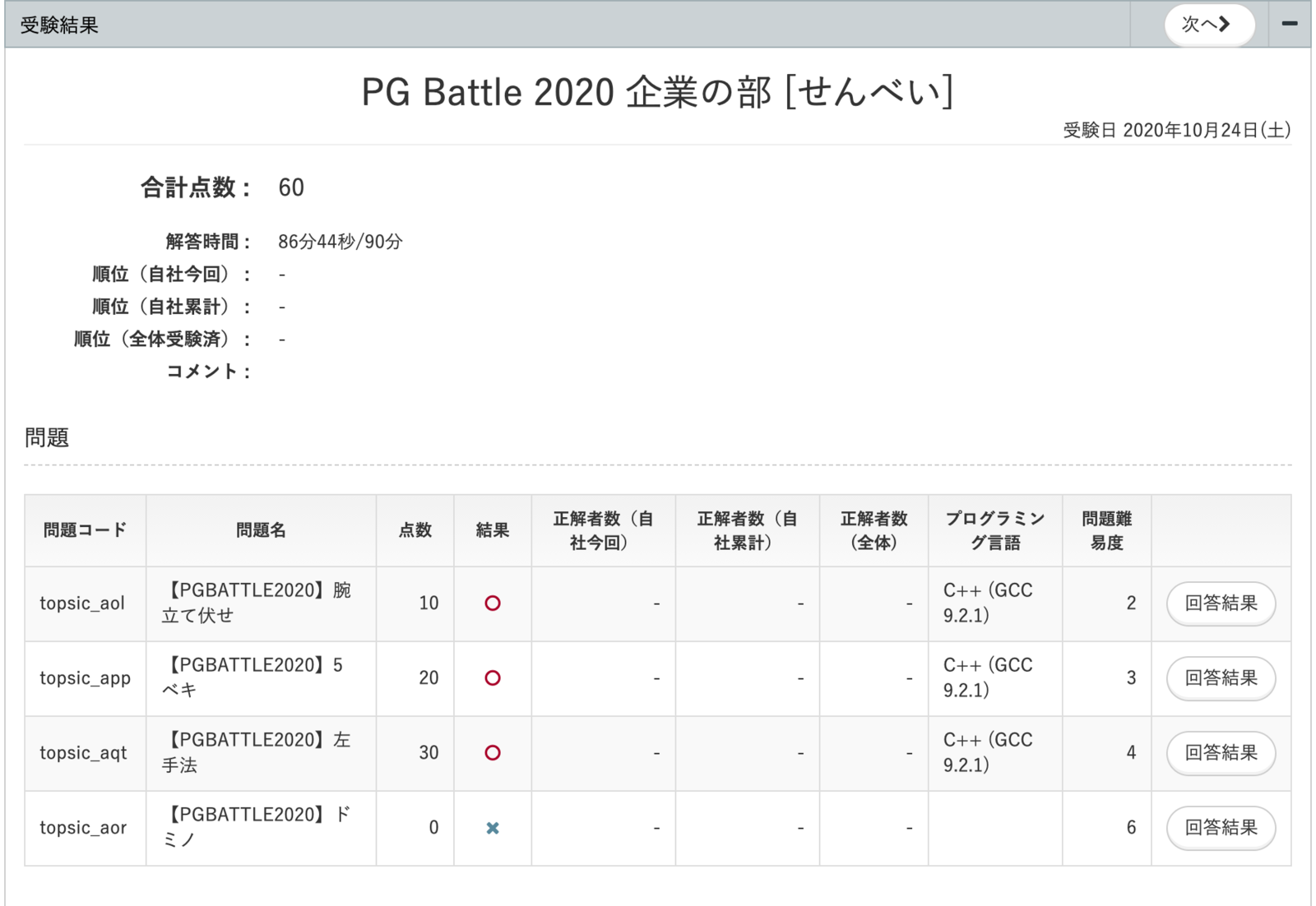
f:id:optim-tech:20201120162707p:plain

解いた問題は落としてなくてよかったです。
30位の企業賞に引っかかったので、自分は図書カードにしました。

かつおぶし

（担当：千坂）

「かつおぶし」担当兼、本記事を執筆している千坂です。
4問中3問提出し、2問正解しました。

1問目行き止まり (Dead End)

【問題概要】

$N$ 個の部屋 $1, 2, \ldots, N$ と、2つの部屋を繋ぐ $N-1$ 個の廊下があり、すべての部屋は廊下を通ることで行き来できます。
部屋 $1$ から始めて廊下を伝って部屋を移動するとき、直前の移動で通った廊下には戻らないようにすると、いずれ移動ができなくなります。
移動ができなくなるときにいる部屋としてありえるものの個数を求める問題です。

【解法】

$N$ 頂点 $N-1$ 辺の連結なグラフは木なので、部屋 $1$ を根とすると、葉の数を答えれば良いです。
根以外で次数が $1$ の頂点は葉なので、それを数えて出力します。

2問目単調増加列 (Increasing Sequence)

【問題概要】

整数 $N, S$ が与えられるので、正整数から成る長さ $N$ の（広義）単調増加列で、総和が $S$ になるものを辞書順ですべて出力する問題です。
$S$ は $50$ 以下です。

【解法】

すべて出力する問題なので、再帰ですべて出力すれば良いです。
求める数列 $\{ a_i \}$ は単調増加列なので $\displaystyle \sum_{k=i}^{N} {a_k} \ge a_i \times \left( N - i + 1 \right)$ を満たします。
これにより、 $a_i$ を決める時点で全体の総和が $S$ を超えないように枝刈りができます。
これで間に合います。

3問目ハンドベル (Handbells)

【問題概要】

$1$ から $N$ のハンドベルがあり、そのうち $M$ 個は壊れていて使えません。
壊れていない $N-M$ 個の中から $1$ 個以上のハンドベルを鳴らすとき、選んだハンドベルの番号が公差 $D$ の等差数列なら良い音色になります。
良い音色となる選び方が何通りあるか求める問題です。
$N \le 10^ {12}, M \le 2 \times 10^ 5, D \le 10^ {12}$ です。

【解法】

この問題は通せなかったので、正しい解法は公式の解説をご覧ください！
以下は自分の考察です。

公差が $D$ の等差数列に含まれる数は $D$ で割った余りが等しいので、ハンドベルの番号を $D$ で割った余りで分けた列について考えます。

高々 $M$ 個の列以外はすべてのハンドベルが使えるので、そのハンドベルの個数を $L$ ( $\displaystyle L = \lfloor \frac{N}{D} \rfloor$ または $\displaystyle \lfloor \frac{N}{D} \rfloor + 1$ ) とすると、作れる等差数列の組み合わせは $\displaystyle \frac{L \left( L + 1 \right)}{2}$ 通りです。
$N$ を $D$ で割った余りを考えれば $\displaystyle L = \lfloor \frac{N}{D} \rfloor$ となる数と $\displaystyle L = \lfloor \frac{N}{D} \rfloor + 1$ となる数は求められるので、壊れている分を引けば組み合わせの数が求まります。

一部が壊れている列は、壊れているハンドベルを $M_{b_1}, M_{b_2}, \ldots , M_{b_l}$ とすると、 $\{1, 2, \ldots, M_{b_1}-1\}, \{M_{b_1}+1, M_{b_1}+2, \ldots, M_{b_2}-1\}, \ldots, \{M_{b_l}+1, M_{b_l}+2, \ldots\}$ という複数の列に分けて考えられます。
それぞれの列の中で作れる等差数列の組み合わせは、その長さを $L$ として $\displaystyle \frac{L \left( L + 1 \right)}{2}$ で求められます。

以上の壊れていない列と壊れている列の組み合わせの数を足し合わせることで、全体の組み合わせの数が求められます。

4問目赤青木 (Red Blue Tree)

【問題概要】

$N$ 頂点で重み付きの木が与えられます。
2つの頂点 $X, Y$ の距離を $D(X, Y)$ とします。
2つの頂点 $P, Q$ を選んだとき、各頂点 $v$ について $D(v, P) \lt D(v, Q)$ のとき頂点 $v$ を赤に、そうでないとき青に塗ります。
赤の頂点と青の頂点の個数が等しくなるような $P, Q$ の選び方が何通りあるか求める問題です。

【解法】

こちらも解けていないので、正しい解法は公式の解説をご覧ください。

所感

3問目を落としたのが痛かったです・・・。
3問目を通していれば、順位が5位ほど上がったのではないかと思います。
とはいえ順位がキリ番で賞品が貰えたので、よしとします。

選べる賞品はワイヤレスイヤホンかホットプレートか枕でかなり迷いました。
1万円相当の枕の寝心地も気になりましたが、最終的にイヤホンを選びました。
オンラインミーティング等でありがたく使わせていただいております。

まとめ

各人の所感にもありますが、結果は 191 チーム中 30 位でした。
まずまずの結果ではありますが、より実力を高められるようにメンバー一同精進していこうと思います。

競プロが得意な方もそうでない方も、オプティムで一緒に働く仲間を募集しています。

PG BATTLE とは

問題の紹介と感想

ましゅまろ

1問目 動物園 (Zoo)

2問目 平均気温 (Average Temperature)

3問目 距離感 (Sense of Distance)

4問目 辞書順最小最短経路 (Minimum Lexicographical Shortest Path)

所感

せんべい

1問目 腕立て伏せ (Push Up)

2問目 5ベキ (Power of 5)

3問目 左手法 (Left-Hand Rule)

4問目 ドミノ (Domino)

所感

かつおぶし

1問目 行き止まり (Dead End)

2問目 単調増加列 (Increasing Sequence)

3問目 ハンドベル (Handbells)

4問目 赤青木 (Red Blue Tree)

所感

まとめ

1問目動物園 (Zoo)

2問目平均気温 (Average Temperature)

3問目距離感 (Sense of Distance)

4問目辞書順最小最短経路 (Minimum Lexicographical Shortest Path)

1問目腕立て伏せ (Push Up)

3問目左手法 (Left-Hand Rule)

4問目ドミノ (Domino)

1問目行き止まり (Dead End)

2問目単調増加列 (Increasing Sequence)

3問目ハンドベル (Handbells)

4問目赤青木 (Red Blue Tree)