深層距離学習(Deep Metric Learning)の基礎から紹介

こんにちは、R&Dチームの河野(@ps3kono)です。深層学習モデルの開発を担当しております。
今回は、画像分類、画像検査、顔認識や異常検知など様々な分野に利用されている深層距離学習(Deep Metric Learning)について紹介したいと思います。

Deep Metric Learningとは
定番のクラス分類と距離学習によるクラス分類の違い
距離学習の進化
- 1. 対照的(contrastive)アプローチ
- 2. Softmaxをベースにしたアプローチ
  - 代表的な学習手法
  - さらなる改善と進化(2019年以降)
推論
深層距離学習の利点と応用
まとめ
おわりに
参考文献

Deep Metric Learningとは

深層距離学習(Deep Metric Learning)とは、サンプル間の距離(metric)または類似度(similarity)に基づいてクラスごとに分離されるよう、入力データを特徴量空間への変換を学習させる手法です。距離学習の目的は、同じクラス（intra-class）のサンプル間の距離を小さくしながら、異なるクラス(inter-class)のサンプル間の距離を大きくすることです。古典的距離学習の代表的な手法としては、マハラノビス距離学習(Mahalanobis Distance Metric Learning)が挙げられます。深層学習の発展に伴い、深層学習と距離学習を組み合わせた様々な深層距離学習手法が提案されています。

定番のクラス分類と距離学習によるクラス分類の違い

まずは、深層学習によるクラス分類の仕組みについて、簡単に説明します。クラス分類用の畳み込みニューラルネットワーク(CNN)の基本構造は、図1のように特徴量抽出(feature extraction)とクラス分類(classification)に分けられます。特徴量抽出の部分は、複数の畳み込み層(convolutional layer: CONV)とpooling層から構造され、最終的にflatten層で一次元化されます。このプロセスで入力画像が特徴ベクトルに変換され、この特徴ベクトルはEmbeddingと呼ばれることがあります。クラス分類の部分では、入力された特徴ベクトルで分類を行い、各クラスの所属確率を予測結果として出力します。定番のCNNでは、この部分が一つまたは複数の全結合層(FC)で構造され、出力されたlogitsをsoftmax関数でクラス所属確率(probability)に変換します。次は、argmax関数で最も確率の高いクラスに予測します。(※ logitsとは、unnormalized log probabilitiesと呼ばれることがあります。)

f:id:optim-tech:20210930131332j:plain:w798 — 図１クラス分類の仕組み

定番のクラス分類と距離学習によるクラス分類の違いは、特徴量抽出部分を学習させる手法にあります。定番のクラス分類の学習ではintra-classとinter-classのサンプル間の距離を考慮せず全結合層で分離可能な(separable)特徴量を取り出すよう特徴量抽出ネットワークを学習させることです(図2)。クラス分類部分は一つのFC層で構造された場合、線形的に分離可能な特徴量を得られます。通常のクラス分類では訓練データに各クラスのサンプル数が十分含まれた場合に高い精度を達成できますが、訓練サンプルの少ないクラスまたは未知クラスがある場合には適していません。一方、距離学習による学習手法は意図的にinter-classのサンプル間の距離を大きくして、intra-classのサンプル間の距離を小さくするように学習させるため、識別的な(discriminative)特徴量を得ることができます(図2)。定番の学習手法と比較すると、intra-classのクラスターがよりコンパクトで、inter-class間の距離がより離れ、識別性の高い特徴量空間へ変換することができるようです¹。そのため、各クラスのサンプルが少ないときや未知クラスがあるときでも十分な性能を発揮でき、顔認識や異常検知タスクなどでよく用いられています。

f:id:optim-tech:20210930131345j:plain:w702 — 図２分離可能な(separable)特徴量と識別的な(discriminative)特徴量

なお、距離学習の目的は識別的な特徴量を抽出することであり、クラス分類の他にクラスタリングタスクにも適用されています。クラス分類の部分は、必ずしもFC層で行う必要がありません。これについては、後述します

距離学習の進化

1. 対照的(contrastive)アプローチ

このアプローチでは、直接的にintra-classのサンプルを引き寄せてinter-classのサンプルを押しのけるように設計された損失関数を利用します。重要な要素は、ネットワーク構造、損失関数とサンプル選択です。まずは、サンプル選択について説明してから、代表的な学習手法ついて紹介します。

サンプル選択(sample selection)

対照的アプローチでは、直接的にサンプル間の距離でロスが計算されたため、サンプル組み合わせの選択はモデル訓練の成功と収束性に大きな影響を与えます。また、全ての可能なサンプル組み合わせで訓練すると、非常に計算量と時間がかかるため、効果的かつ効率的な学習のためには有益なサンプル組み合わせを選択することが重要です。代表的な手法は図3に示されます。簡単なサンプル組み合わせ(Easy negative mining)は、訓練に効果が少なく、時間と計算リソースの無駄使いに繋がると先行研究²で分かっていました。そのため、対照的アプローチの距離学習ではsemi-hardまたはhard negative miningがよく使われているようです。詳細については、「Deep metric learning: A survey」³の論文をご参考してください。

f:id:optim-tech:20210930180520j:plain:w599 — 図３Negative miningの種類

上記の図では、 $x^a$ は基準となるサンプル(anchor)で、 $x^p$ は $x^a$ と同じクラス(positive)のサンプルで、 $x^n$ は異なるクラス(negative)のサンプルとなります。 $D(x^a, x^b)$ はサンプル $x^a$ と $x^b$ の間の距離です。マージン( $m$ )は、正の定数であるハイパーパラメータです。

代表的な学習手法

Contrastive loss

Contrastive lossは、2006年に次元削減(Dimensionality Reduction)の目的で提案され⁴、一緒に使われる代表的なネットワーク構造はSiamese networkです(図4)。2枚の画像ペアを入力して、共有重み(shared weights)のネットワークで特徴量を抽出し、その距離( $D$ )によってネットワークを学習させます。intra-classのペア(positive)を入力したときは距離を最小化するように学習し、inter-classのペア(negative)を入力したときは、距離を最大化するようネットワークを学習させます。損失関数は、下記のとおりです。

$\begin{align} L_{Contrastive}&=(1-Y)\cfrac{1}{2}(D)^2+(Y)\cfrac{1}{2}{max(0, m-D)}^2 \\ D(x_i^a, x_i^b)&=\|f(x_i^a)-f(x_i^b)\|_2 \end{align}$

${x_i}^a$ と ${x_i}^b$ は、 $i$ -th入力画像のペアです。 $Y$ はペアのラベルであり、positiveペアの場合は0でラベルされ、negativeペアの場合は1でラベルされます。マージン( $m$ )は、正の定数であるハイパーパラメータです。上記の式によると、positiveペアを入力する場合は、 $D=0$ になるよう学習させ、negativeペアを入力する場合は $D>m$ になるよう学習させます。ただし、クラス内またはクラス間の距離はクラスごとに異なり、大きく変動する可能性があるため、すべてのnegativeペアに一定のマージンを適用することは不適切だと思われます。

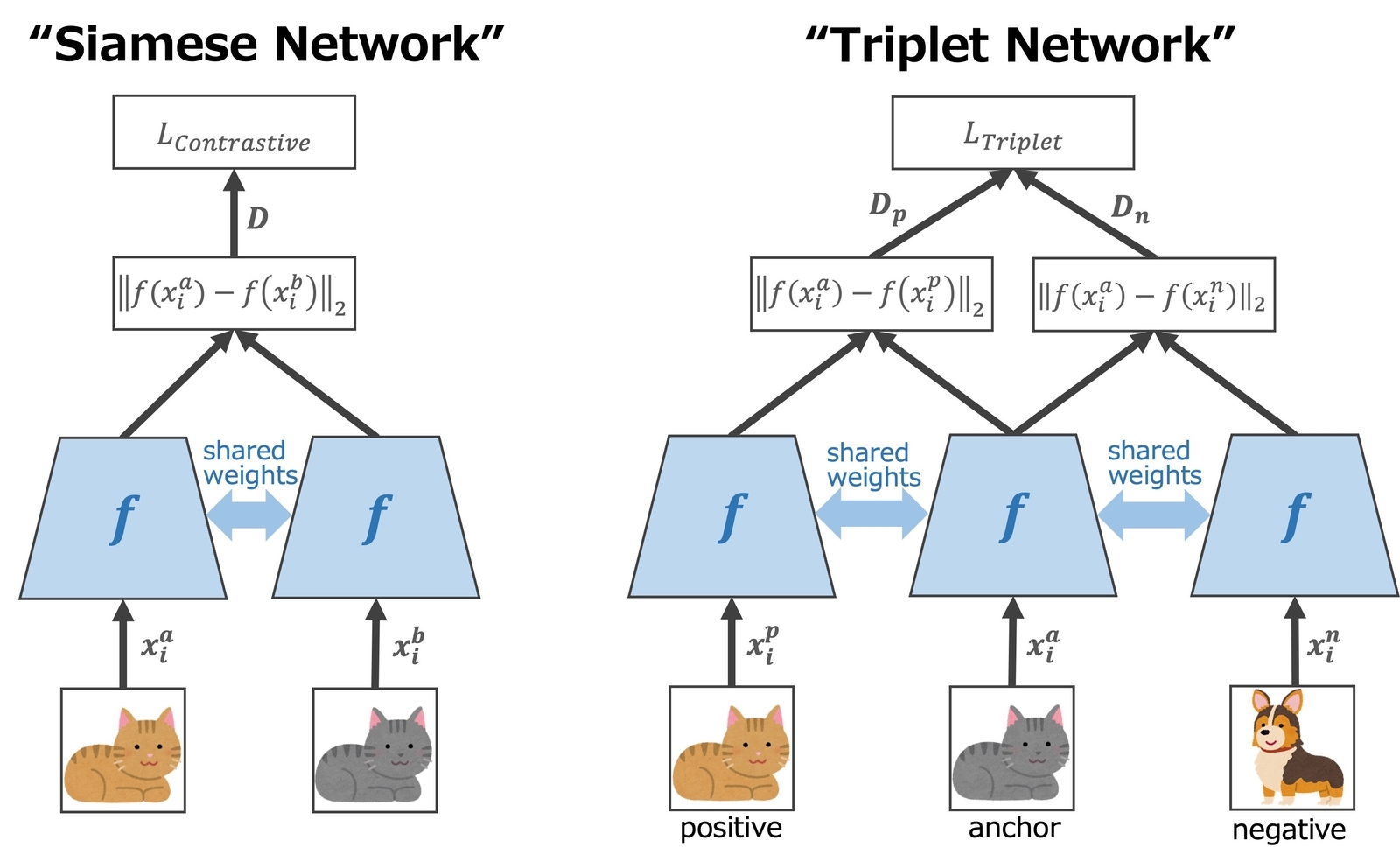
f:id:optim-tech:20210930131338j:plain:w797 — 図４対照的アプローチのネットワーク構造

Triplet loss

Triplet lossでは、相対距離にマージンが適用されたため、Contrastive lossにおけるマージンの課題に対処することができます。Contrastive lossのように絶対距離にマージンをかけるのではなく、3枚組の入力画像でpositiveペアとnegativeペアの相対距離を算出し、それにマージンをかけます。つまり、Contrastive lossではnegativeペアをマージン $m$ の距離よりも離れるように学習させることですが、Triplet lossではnegativeサンプルとの距離をpositiveサンプルとの距離よりもマージン $m$ の距離以上遠くなるよう学習させることです。同時で、intra-classのサンプルを引き寄せてinter-classのサンプルを離れようとすることができます。現在でも広く使われている距離学習手法のようです。

先行研究では、Triplet lossの損失関数としていくつかの微妙な違いのある式が使用されていましたが、その中によく引用されたのはWang et al.(2014)⁵のようです。その損失関数は下記の式で表されます。

$L_{Triplet}=max(0, D^2(x_i^a, x_i^p)-D^2(x_i^a, x_i^n)+m)$

${x_i}^a$ 、 ${x_i}^p$ 、 ${x_i}^n$ は $i$ -thサンプル組の基準となるanchor画像、positive画像とnegative画像です。この論文ではHinge lossと呼ばれましたが、最近の研究では同様な式をTriplet lossと呼ばれることが多いようです。FaceNetの論文²⁰は、上記の式をもとにして最小化される損失関数をTriplet lossとして提案しました。下記の式では、最小損失をゼロに設定しています。

$L_{Triplet}=\sum_i^N\left[\|f(x_i^a)-f(x_i^p)\|_2^2-\|f(x_i^a)-f(x_i^n)\|_2^2+m\right]_+$

なお、上記の2つの論文では、サンプル間の距離を比較するために正規化された特徴量を用いています。Triplet lossと一緒に使われている代表的なネットワーク構造はTriplet networkです(図4)。

さらなる改善と進化

Triplet lossの主な制限の一つは、ロスを計算するためにanchorとあるクラスからのnegativeサンプルとしか比較されず、他クラスのnegativeサンプルが無視されることです。例えば、クラスA〜Eがあるとしたら、 $i$ -thの反復で、クラスAのサンプルがanchorとして選ばれ、クラスBのサンプルがnegativeサンプルとして選ばれた場合、クラスAとクラスBの間の距離のみでロス計算しネットワーク重みを更新することになります。この制限を克服することを目的として、複数クラスのnegativeサンプルを同時に比較できる損失関数がいくつか提案されています。Quadruple loss、Structured loss、N-pair loss、NT-Xent loss(N-pair lossの改良版⁶)、Magnet loss、Clustering loss、Mixed lossなど。詳細については、参考文献^3,7をご参照してください。もう一つの問題は、クラス内とクラス間のサンプル間の距離はクラスごとに異なるため、上記のように一定のユークリッド距離のマージンを指定することが不適切だと思われます。この問題を解決するためにスケールに依存しないAngular lossが提案されました⁸。この損失関数は、距離の代わりにサンプル間の角度を比較します。

また、損失関数の改善以外にも、Distance Weighted Sampling⁹やDeep Adversarial Metric Learning¹⁰などのnegative miningを改善する方法がいくつか提案されています。

対照的アプローチの問題点

学習の成功と収束性はサンプル選択に大きく依存し、アルゴリズム設計に手間がかかります。
慎重なサンプル選択が必要なため、アルゴリズムが複雑になる傾向があります。
サンプル間の距離でロスを計算するため、入力になっているサンプルの組数が劇的に増加します。
サンプル組の中またはmini-batchの中でサンプル間の距離を比較して重みを更新するため、グローバルではなくローカル情報で学習することになります。（この問題を解決するために、Clustering lossとMagnet lossが提案されましたが、精度の問題や複雑さにより人気がなかったようです）

2. Softmaxをベースにしたアプローチ

このアプローチは近年(2016年以降)に提案され、クラス分類用のSoftmax lossに基づいた手法です。Softmax lossの式は、下記のとおりとなります。

$\begin{align} L_{Softmax}=-\cfrac{1}{N}\sum_{i=1}^N log(\cfrac{e^{W_{y_i}^Tx_i+b_{y_i}}}{\sum_{j=1}^ne^{W_j^Tx_i+b_j}}) \end{align}$

$x_i$ は $i$ -thサンプルの特徴量であり、 $y_i$ -thクラスに所属しています。 $W_j$ と $b_j$ は $j$ -th列の重みとバイアスです。

Softmax lossは、同クラスのサンプル間の類似度を高めながら他クラスの類似度を低くするように強制しないため、得られた特徴量でのクラス識別性能は低いという課題があります。それを対処するために、いくつかの損失関数が以下のように提案されています。

代表的な学習手法

Center loss

2016年に、同クラスのサンプル間の距離を短縮するよう特徴量とそれに対応するクラスの中心位置との距離でペナルティを課すCenter lossがWen et al.(2016)¹で提案されました。上記の対照的アプローチのような直接的にサンプル間の距離を比較する学習手法と違って、このアプローチではグローバルな情報(クラス中心位置)を利用して学習することが可能になり、さらに面倒なサンプル選択の工夫が不要になります。Center lossの損失関数( $L_{Center}$ )は下記のとおりで、訓練時にはSoftmax lossに加算した損失関数( $L_{total}$ )を使われています。

$\begin{align} L_{Center}&=\cfrac{1}{2}\sum_{i=1}^{N}\|x_i-c_{y_i}\|_2^2 \\ L_{total}&=L_{Softmax}+\lambda L_{Center} \\ &=-\sum_{i=1}^N log(\cfrac{e^{W_{y_i}^Tx_i+b_{y_i}}}{\sum_{j=1}^ne^{W_j^Tx_i+b_j}})+\cfrac{\lambda}{2}\sum_{i=1}^{N}\|x_i-c_{y_i}\|_2^2 \end{align}$

$c_{y_i}$ は $i$ -thサンプルの正解クラス( $y_i$ -thクラス)の中心位置です。各クラスの中心位置( $c_{j}$ )はmini-batchごとで更新され、2つの損失関数のバランスをとるためにパイパーパラメータ $\lambda$ が導入されました。クラス中心位置の不適切な定義や更新の困難さなどによりCenter lossはあまり普及しませんでしたが、以下のようなState-of-the-Art手法の発展に大きく影響を与えました。

SphereFace

SphereFaceの論文¹¹では、Softmax lossで学習した特徴量には固有の角度分布があることが示唆され、Center lossのようにユークリッド距離で比較するよりも、角度距離で比較すべきだと提案されました。損失関数はSoftmax lossをベースにし、以下のように改良されています。

1. バイアス( $b$ )をゼロにし、 $\|W_j\|=1$ になるよう重み( $W$ )を列で正規化する。

2. 識別力を高めるようハイパーパラメータとしてMultiplicative angular margin( $m$ )を導入する。

その結果、SphereFaceの損失関数は以下となります。

$\begin{align} L_{SphereFace}=-\cfrac{1}{N}\sum_{i=1}^N log(\cfrac{e^{\|x_i\|\cos(m\theta_{y_i,i})}}{e^{\|x_i\|\cos(m\theta_{y_i,i})}+\sum_{j\not=y_i} e^{\|x_i\|\cos(\theta_{j,i})}}) \end{align}$

$x_i$ は、 $i$ -thサンプルの特徴量です。 $W_j$ は重みの $j$ -th列であり、概念的に $j$ -thクラスの中心位置だと考えられます。Angular margin( $m$ )は特徴量( $x_i$ )と重みの $y_i$ -th列との角度( $\theta_{y_i,i}$ )に対してのみ適用されます。この手法では、特徴量が正規化されず重みのみが正規化されます。ネットワーク構造はFig.5と似ていますが、特徴量の正規化とスケーリング部分はありません。なお、他手法の損失関数と容易に比較できるよう、一般化された式ではなく上記の式で説明しました。

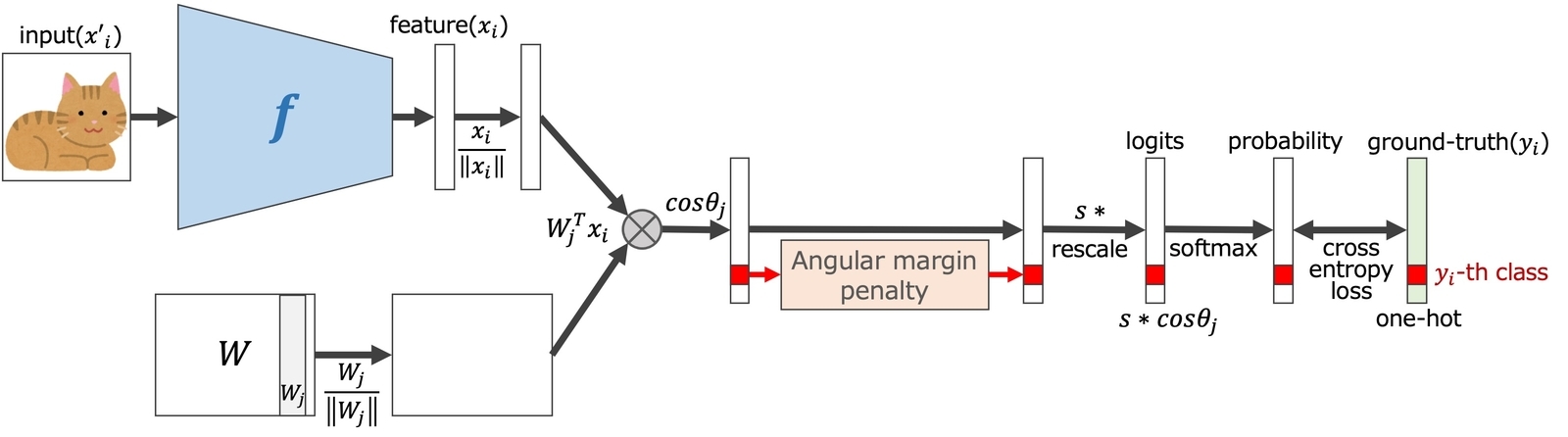
f:id:optim-tech:20210930131412j:plain:w881 — 図５CosFaceとArcFaceのネットワーク構造

CosFace

CosFace¹²では、SphereFaceアルゴリズムが下記のように改良されました。

1. 重み( $W$ )と同様に特徴量( $x_j$ )を正規化する。SphereFaceと同様に $b=0$ のため、最後のFC層の出力は $W_j^Tx_i=\|W_j\|\|x_i\|cos(\theta_{j,i})=cos(\theta_{j,i})$ になる。 $\theta_{j,i}$ は特徴量 $x_i$ と $j$ -thクラスの中心位置 ( $W_j$ )との角度距離となる。つまり、 $\cos(\theta_{j, i})$ は特徴量 $x_i$ と $j$ -thクラスの中心位置とのコサイン類似度である。

2. スケーリングパラメータ( $s$ )をハイパーパラメータとして導入することで、収束性を向上させる。

3. さらに識別力を高めるために、Cosine marginをAngular marginとして導入する。Cosine marginはMultiplicative angular marginと違って $\theta_{j, i}$ によって変化したり、 $\theta_{j, i}=0$ で消失したりしないため、全てのサンプルに一貫して適用することが可能。SphereFaceと同様に、Cosine marginは特徴量( $x_i$ )と正解クラスの中心位置( $W_{y_i}$ )とのコサイン類似度( $\cos(\theta_{y_i,i})$ )に対してのみ適用される。

ネットワークの構造は図5と同様であり、損失関数は以下のように表せます。　

$\begin{align} L_{CosFace}=-\cfrac{1}{N}\sum_{i=1}^N log(\cfrac{e^{s(\cos(\theta_{y_i,i})-m)}}{e^{s(\cos(\theta_{y_i,i})-m)}+\sum_{j\not=y_i} e^{s\cos(\theta_{j,i})}}) \end{align}$

ArcFace

ArcFace¹³の損失関数は、CosFaceとほとんど似ていて、ただ一つの違いはマージン $m$ の定義です。コサイン空間ではなく、直接的に角度空間でマージンを加算したため、線形な分離境界を確保できます。このマージンは、Additive angular marginと呼ばれます。ネットワークの構造は図5に示し、損失関数は以下のとおりです。

$\begin{align} L_{ArcFace}=-\cfrac{1}{N}\sum_{i=1}^N log(\cfrac{e^{s(\cos(\theta_{y_i,i}+m))}}{e^{s(\cos(\theta_{y_i,i}+m))}+\sum_{j\not=y_i} e^{s\cos(\theta_{j,i})}}) \end{align}$

ArcFaceとCosFaceでは、スケーリングパラメータ $s$ とマージン $m$ のハイパーパラメータがあり、性能を最適化するために適切な値に設定する必要があります。また、ArcFaceの論文では、SphereFaceとCosFaceとArcFaceを組み合わせた損失関数を提案しており、その組み合わせた損失関数は以下に示します。

$\begin{align} L_{combine}=-\cfrac{1}{N}\sum_{i=1}^N log(\cfrac{e^{s(\cos(m_1\theta_{y_i,i}+m_2)-m_3)}}{e^{s(\cos(m_1\theta_{y_i,i}+m_2)-m_3)}+\sum_{j\not=y_i} e^{s\cos(\theta_{j,i})}}) \end{align}$

$m_1$ は SphereFace のMultiplicative angular margin、 $m_2$ は ArcFace のAdditive angular margin、 $m_3$ は CosFace のCosine marginに相当します。

さらなる改善と進化(2019年以降)

AdaCos(2019年)¹⁴の論文では、スケーリングパラメータ $s$ とマージン $m$ のパラメータ調整の効果について徹底的に評価され、それらのハイパーパラメータを自動的に調整するAdaCos lossを提案されました。
Circle loss(2020年)¹⁵は、類似度スコアに応じてペナルティの強さを調整し、動的にペナルティを適用する損失関数です。対照的アプローチとSoftmaxをベースにしたアプローチ用の損失関数が提案されました。
ArcFaceの改良版
- Sub-center ArcFace¹⁶は、ノイズ(難しいサンプル)の多いデータへの対策として、複数のクラス中心位置を定義した手法です。
- ArcFace用の動的マージン¹⁷は、極端な不均衡データセットに対応するため、Google Landmark Recognition 2020 Competitionの第3位の受賞者によって提案されたものです。
- Dyn-arcFace¹⁸では、過学習しにくくするよう、動的なAdditive angular marginが導入されました。
MagFace(2021年)¹⁹は、顔認識専用に提案され、得られた特徴量は高い識別性を持つだけでなく、特徴ベクトルの大きさによって顔画像の質を示すことができます。学習時には、簡単なサンプルはクラス中心位置に引き寄せられ、難しいサンプルは押しのけられます。

推論

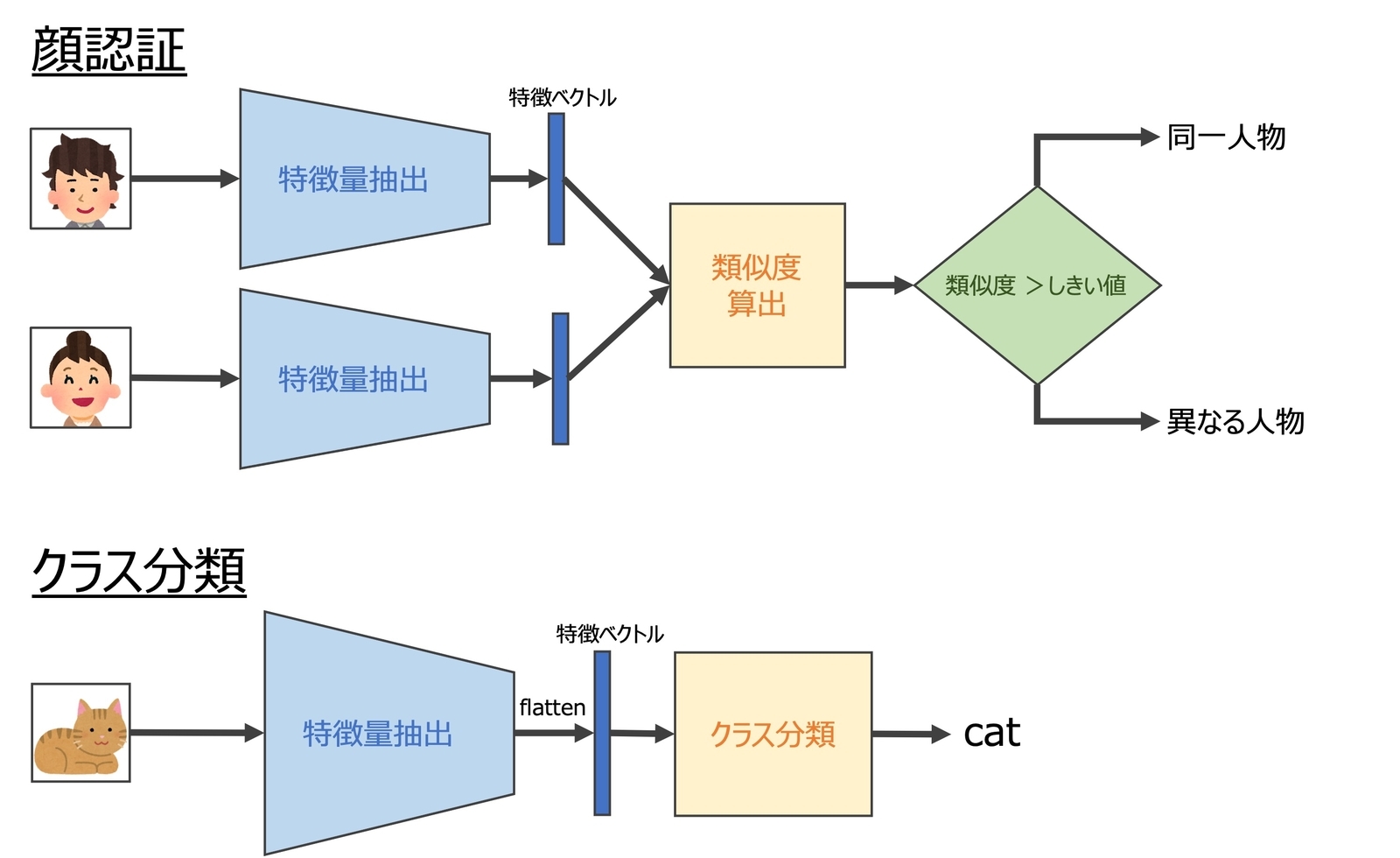
距離学習の主な目的は、入力画像を識別性の高い特徴量に変換する特徴量抽出器(図4-5の $f$ )を得ることです。得られた特徴量をどのように利用するかは、用途によって異なります。例えば、顔識別では、入力画像と参照画像から抽出した特徴量を比較し、同一人物の画像であるか異なる人物の画像であるかを検証します(図6)。分類タスクでは、得られた特徴量を分類器に入力し、どのクラスに属するかを判断します。一つの方法としては、特徴量と各クラスの中心位置との距離を比較し、コサイン類似度が最も高い(または距離が最も小さい)クラスを予測クラスに割り当てることです。

f:id:optim-tech:20210930131351j:plain:w745 — 図６推論方法

深層距離学習の利点と応用

定番の分類モデルとは異なり、識別性の高い特徴量を得ることができるため、極端に不均衡なデータセット(異常検知、医用画像診断など)や、Few-Shot learning(顔認識、手書き認識、音声認識など)や、Zero-Shot learning(訓練データに存在しないクラスを扱う必要があるタスク)などに対応できます。
クラス数に応じてサイズが大きくなる分類用のFC層が不要になるため、クラス数が多いタスクではモデルサイズがより小さくなります。

まとめ

深層距離学習は、識別性の高い(discriminative)特徴量を得るためにディープニューラルネットワークを学習させる手法です。得られたモデルは特徴量抽出器として利用します。
不均衡データやFew-ShotとZero-Shot learningなどの課題でよく使われています。
学習手法は大きく、対照的アプローチとSoftmaxをベースにしたアプローチに分けられます。それらの代表的な手法としては、Triplet lossとArcFaceが挙げられます。
対照的アプローチの手法では、サンプルの組を入力データとし、正解ラベルはペアの種類(positive/negative)となります。一方、Softmaxをベースにしたアプローチでは、定番のクラス分類と同様に、入力と正解ラベルは入力画像とそのクラスラベルとなります。
対照的アプローチでは、損失関数の設計の他に、サンプル選択の設計も大事です。
Softmaxをベースにしたアプローチでは、訓練時で特徴量抽出器と全クラスの中心位置に相当した重み $W$ を同時で学習させたため、推論時でクラス分類をしたい場合はその重みを利用できます。(訓練データに存在しないクラスがある場合は対応不可)
本記事では画像データの分析で説明しましたが、入力データは画像に限られません。

おわりに

OPTiMでは、AIとIoT技術でビジネス課題・社会的課題を解決したい、チャレンジ精神・向上心を持っているエンジニアを積極的に募集してます。農業・医療・建設・産業分野などにおいてAIやIoTの活用で推進しているため、関心のある技術領域に挑戦するチャンスがあります。興味のある方は、こちらをご覧ください。 www.optim.co.jp