はじめまして、R&D チームの宮城です。業務では主に画像分類モデルの開発や精度改善を担当しており、現時点(2021年3月)でR&D唯一の文系学部出身です。
趣味はNBA観戦で、ジョージ・ワシントン大学時代の渡邊雄太選手(現トロント・ラプターズ)を生で見たことがあります。自分と同じ人間とは思えないほどスタイルが良くハンサムでした。

今回の記事ではDeep Learningを用いた分類タスクにおいて、順序をもつクラス分類（統計学でいう「順序尺度」によるクラス分類）の誤差をうまく計算できる label distribution learning という手法を紹介します。

誤差を算出する損失関数から順を追って説明していきますので、直接 label distribution learning の項目から読み進めていただいても結構です。

損失関数
- 損失関数とは
- cross entropy loss
one-hotな確率分布をもつ正解データの問題点
- 分類クラスが順序をもたない場合
- 分類クラスが順序をもつ場合
label distribution learning
おまけ
- weighted kappa loss
おわりに
ライセンス表記

損失関数

損失関数とは

モデルの「推定」と「正解」の誤差を計算する関数です。ニューラルネットワークは学習時、損失関数によって計算された誤差が最も小さくなるようパラメータを探索・更新します。

cross entropy loss

cross entropy loss は分類タスクでよく使われる損失関数です。cross entropy は２つの確率分布の類似度を評価する指標であり、cross entropy loss によって計算される誤差 $E$ は真の確率分布 $p$ 、推定した確率分布 $q$ を用いて下記の通り表せます。

$\begin{aligned} E = - \sum_{x} p(x) \log(q(x)) \end{aligned}$

one-hotな確率分布をもつ正解データの問題点

分類タスクにおいて、正解データは正解クラスの確率が1、不正解クラスの確率が0となるone-hotな確率分布で与えられることが多いですが、分類クラスが順序をもつ場合、使用する損失関数によってはクラス間の誤差をうまく調整できないことがあります。

分類クラスが順序をもたない場合

まずは分類クラスが順序をもたない場合(統計学でいう「名義尺度」によるクラス分類)について具体例を使って説明します。

入力画像を

①犬🐶
②猿🐵
③キジ🐦

の3クラスに分類するモデルを例に cross entropy loss による誤差を計算してみます。

正解クラス(入力画像)が ②猿🐵 で、モデルの推定した確率分布 $q$ が

$(①犬🐶:0.2, \ ②猿🐵:0.7, \ ③キジ🐦:0.1)$ であるとします。

正解データがone-hotな確率分布をもつ場合、真の確率分布 $p$ は

$(①犬🐶:0, \ ②猿🐵:1, \ ③キジ🐦:0)$ です。

正解クラスの確率が1、不正解クラスの確率が0となるため正解クラスの推定確率 $q(k)$ だけが残り、式は下記の通りシンプルになります。

$\begin{aligned} E %= - \sum_{x} p(x) \log(q(x)) \\ &= - \log(q(k)) \end{aligned}$

よってcross entropy lossは

$\begin{aligned} E &= - \log(q(k)) \\ &= - \log(0.7) \\ &\fallingdotseq 0.357 \end{aligned}$

となります。cross entropy lossの計算には正解クラス②猿🐵 の推定確率:0.7 しか使用されていないことが確認できます。
不正解クラスの推定確率という情報を切り捨てていますが、①犬🐶、②猿🐵、③キジ🐦 のように分類するクラスが独立しており順序をもたない場合は特に問題ないように思います。

分類クラスが順序をもつ場合

では次のように、分類するクラスが順序(連続性)をもつ場合はどうでしょうか。

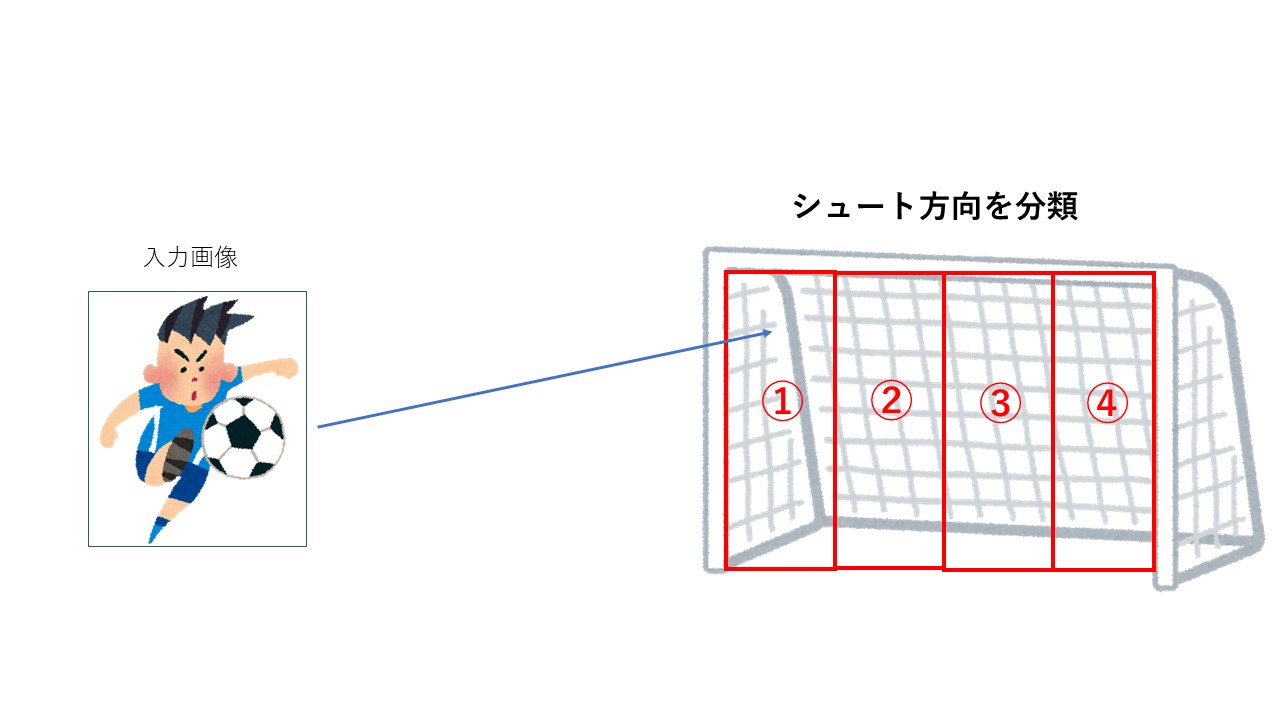
f:id:optim-tech:20210315142456j:plain

サッカーのPK(ペナルティキック)を例に、上図のようにシュート直前のキッカーを入力画像とし、ゴールを4分割してシュート方向を分類するモデルについて考えます。このモデルの分類クラスは

①左端
②中央左
③中央右
④右端

となります。具体例を使ってcross entropy lossを計算していきます。

例1.正解クラスが ①左端で推定クラスが ②中央左、モデルの推定した確率分布 $q$ が $(①左端:0.1, ②中央左:0.7, ③中央右:0.1, ④右端:0.1)$ の場合

cross entropy lossは

$\begin{aligned} E &= - \log(q(k)) \\ &= - \log(0.1) \\ &\fallingdotseq 2.303 \end{aligned}$

例2.正解クラスが ①左端で推定クラスが ④右端、モデルの推定した確率分布 $q$ が $(①左端:0.1, ②中央左:0.1, ③中央右:0.1, ④右端:0.7)$ の場合

cross entropy lossは

$\begin{aligned} E &= - \log(q(k)) \\ &= - \log(0.1) \\ &\fallingdotseq 2.303 \end{aligned}$

例１、例2ともに正解クラス ①左端の推定確率: 0.1 のため cross entropy loss は等しく、2.303となっています。
しかし、この2例を同じ誤差として扱うことは妥当でしょうか。
正解と推定結果を図示した下図を見ると、例1はキーパーがちょっと手を伸ばせば防げそうですが、例2は完全に読みが外れておりゴールを割られることは確実でしょう。直観的には例1よりも例2の方が推定と正解の誤差が大きいと言えそうです。

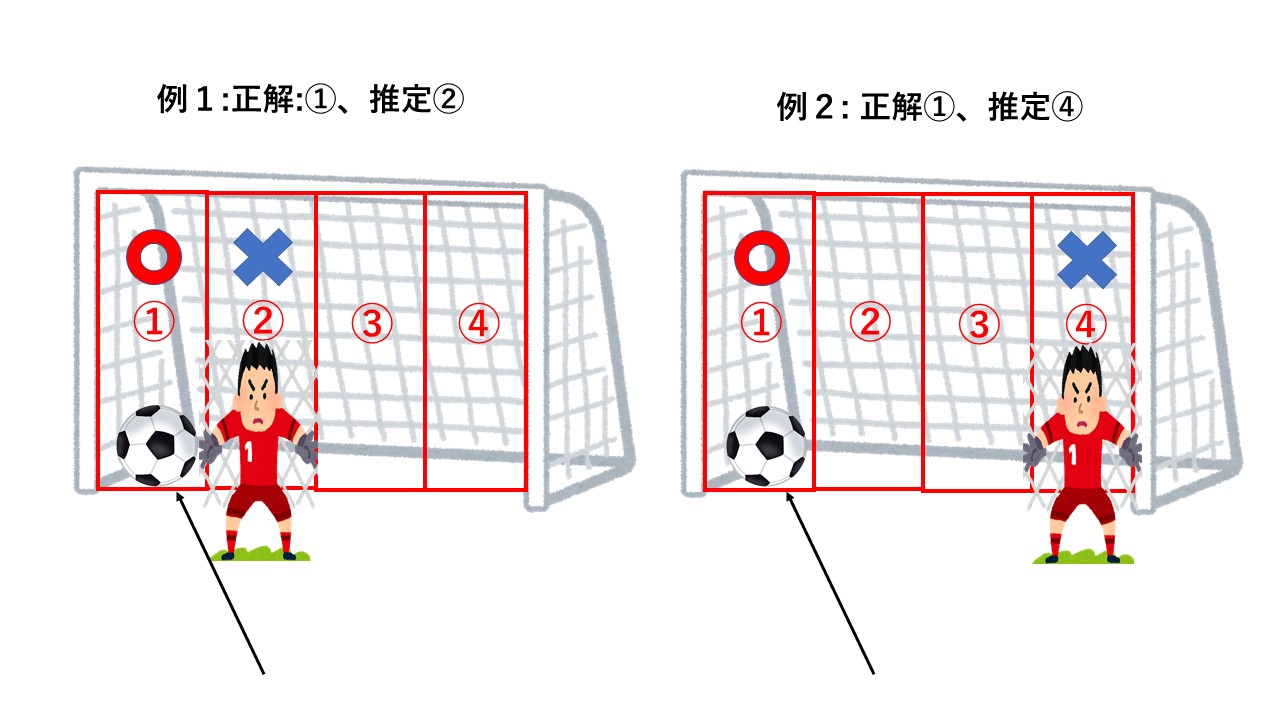
f:id:optim-tech:20210315152325j:plain

このように分類するクラスが順序をもつ場合、小さく間違えた時よりも大きく間違えた時の方が誤差が大きくなるように間違え方に優劣をつけたくなります。
しかし正解データがone-hotな確率分布をもつ場合、cross entropy lossは正解クラスの推定確率のみを使用するため不正解クラスの情報によって誤差を調整することができません。

label distribution learning

前置きが長くなりましたが、順序をもつクラス分類で誤差をうまく計算する手法、 label distribution learning について説明します。下記の論文を参考にしました。

Gao, B. B., Xing, C., Xie, C. W., Wu, J., & Geng, X. (2017). Deep label distribution learning with label ambiguity. IEEE Transactions on Image Processing, 26(6), 2825-2838.

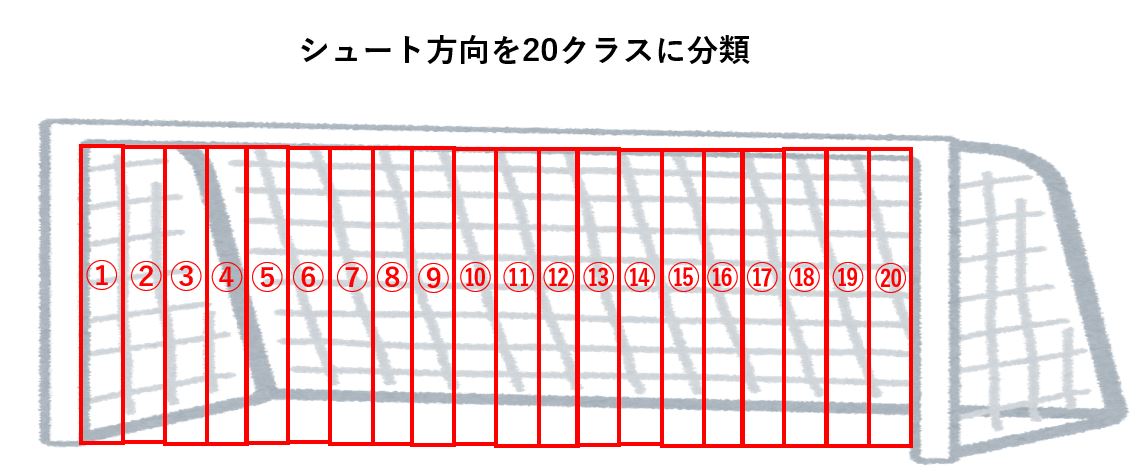
引き続きペナルティキックの方向予測を例に使いますが、label distribution learningは多クラス分類でよく使われるので分類するシュート方向を下図の通り20クラスに増やして説明します。

f:id:optim-tech:20210319180148j:plain

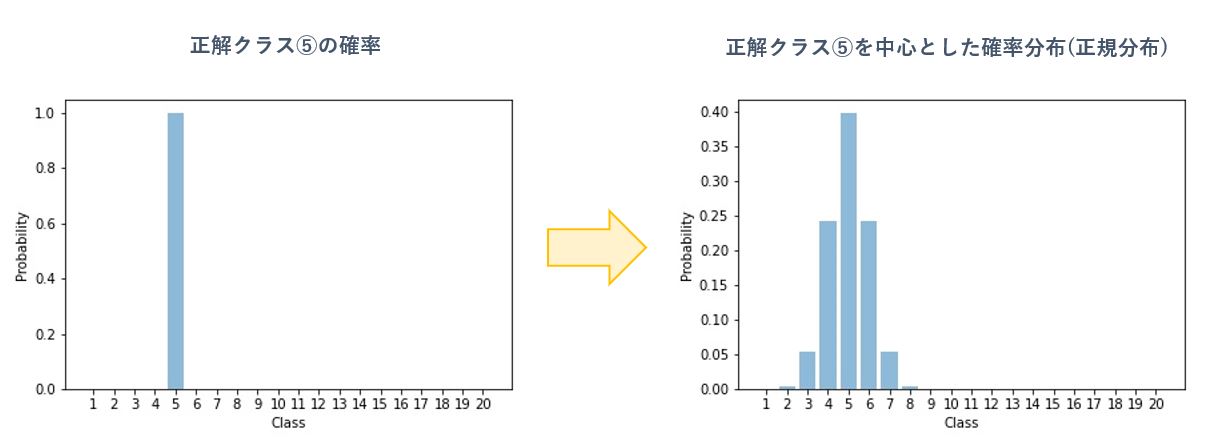
label distribution learning は正解データを、正解クラスの確率=1 、不正解クラスの確率=0 といったone-hotな確率分布を、下図のように正解クラスを中心とした正規分布に変換して学習させます。ここでは正解データについて平均が正解クラス、標準偏差が１の正規分布に従うと仮定します。

f:id:optim-tech:20210319180151j:plain

label distribution learning によって正規分布に変換した正解と推定の誤差を cross entropy loss を使って実際に計算してみましょう。TensorFlowのCategoricalCrossentropy関数を使って実装しました。
実装については下記の注意点にご留意ください。

参考論文では損失関数に Kullback Leibler divergenceを使っていますが、説明をシンプルにしたいため前述の cross entropy loss を使用
分布の違いを分かりやすくするために正解データだけでなく推定データも平均が推定クラス、標準偏差が１の正規分布に従うと仮定

例1.正解クラスが ⑤ で推定クラスが ⑩ の場合

label distribution learning による loss 算出サンプルコード1

import numpy as np
import tensorflow as tf

# 正規分布の値を計算する関数
def calc_normal_distribution(x, mu, sigma=1):
    return 1 / (sigma * np.sqrt(2 * np.pi)) * np.exp(-np.square(x - mu) / (2 * np.square(sigma)))

# 正解クラス⑤を正規分布に変換
y_true = np.array([calc_normal_distribution(i, 5) for i in range(1, 21)])

# 推定クラス⑩を正規分布に変換  
y_pred = np.array([calc_normal_distribution(i, 10) for i in range(1, 21)])

ce_loss = tf.keras.losses.CategoricalCrossentropy()
print(f'ce_loss = {ce_loss(y_true, y_pred).numpy()}')

出力結果1

ce_loss = 12.661133766174316

例2.正解クラスが ⑤ で推定クラスが ⑱ の場合

label distribution learning による loss 算出サンプルコード2

import numpy as np
import tensorflow as tf


# 正規分布の値を計算する関数
def calc_normal_distribution(x, mu, sigma=1):
    return 1 / (sigma * np.sqrt(2 * np.pi)) * np.exp(-np.square(x - mu) / (2 * np.square(sigma)))

# 正解クラス⑤を正規分布に変換
y_true = np.array([calc_normal_distribution(i, 5) for i in range(1, 21)])

# 推定クラス⑩を正規分布に変換  
y_pred = np.array([calc_normal_distribution(i, 18) for i in range(1, 21)])

ce_loss = tf.keras.losses.CategoricalCrossentropy()
print(f'ce_loss = {ce_loss(y_true, y_pred).numpy()}')

出力結果2

ce_loss = 16.118072509765625

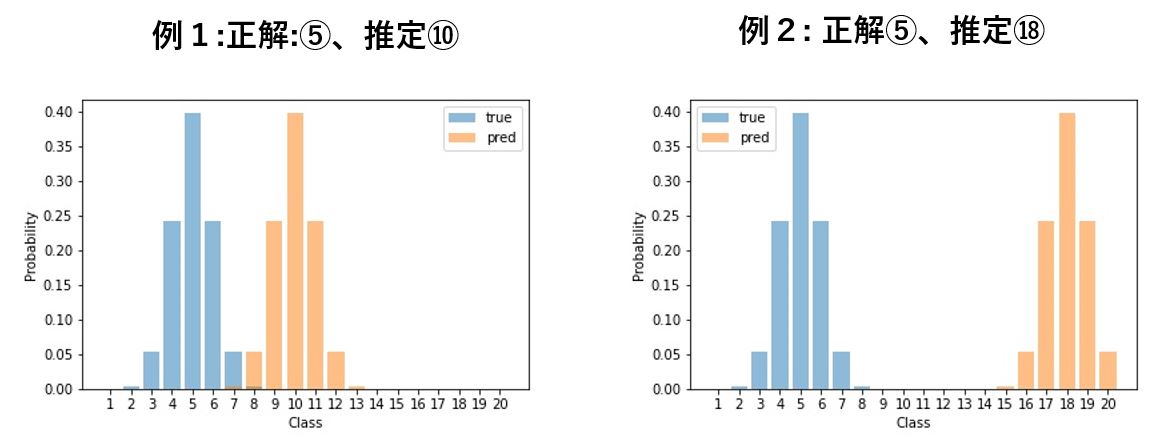
下図は例１、例2における推定、正解の確率分布を図示したものです。（正解の分布が水色の「true」、推定の分布がオレンジ色の「pred」）
例2の方が推定と正解の分布の距離が大きいことが確認できます。

label distribution learning による誤差は例1(12.661) < 例2(16.118) となり、より大きく間違えている例2の誤差を大きく算出できています。
このように label distribution learning は順序をもつクラス分類タスクにおいて、クラス間の距離を誤差に反映できる有効な手法です。

f:id:optim-tech:20210322110435j:plain

おまけ

weighted kappa loss

参考までに、正解データの確率分布が one-hot な場合でも、順序をもつクラス分類の誤差をうまく計算できる損失関数 weighted kappa loss を簡単に説明します。下記の実装を参考にしました。

weighted kappa係数 $k$ はデータの一致度を図る評価指標の一つであり、次の式で定義されます。

$\begin{aligned} k = 1 - \frac{\sum_{i,j} w_{i,j} O_{i,j}}{\sum_{i,j} w_{i,j} E_{i,j}} \end{aligned}$

ここで $i$ は正解クラス、 $j$ は推定クラス、 $w$ は重み(weight)を表します。weightの計算にはクラス間の差をそのまま使用する方法とクラス間の差の二乗を使用する方法がありますが、ここでは重みを二乗で計算することにします。

$\begin{aligned} w_{i,j} = (i - j)^2 \end{aligned}$

再び下図の通り4クラスのシュート方向分類を例に説明します。 f:id:optim-tech:20210315152325j:plain

例えば、クラス ①左端と ④右端間の重みは

$\begin{aligned} w_{1,4} &= (1 - 4)^2 \\ &= 9 \end{aligned}$

となります。

また、 $O_{i,j}$ は正解クラス $i$ と推定クラス $j$ が実際に一致した確率を表し、

$E_{i,j}$ は正解クラス $i$ と推定クラス $j$ が偶然一致する確率を表します。

weighted kappa係数 $k$ は $-1 \leqq k \leqq 1$ の値を取り、正解と推定のデータ類似度が大きければ大きいほど、言い換えると正解と推定の誤差が小さければ小さいほど値が大きくなります。
よって weighted kappa loss によって出力される最終的な誤差 $E$ は下記のように算出し、正解と推定の誤差が小さくなるとlossも同じく減少するようにします。

$\begin{aligned} E = \log(1 - k + \epsilon) \end{aligned}$

$\epsilon$ は $\log0 = - \infty$ を防ぐための補正値で、TensorFlow実装でのデフォルト値は $\epsilon = 1e -6$ です。

先程のシュート方向を①左端、②中央左、③中央右、④右端の4クラスに分類するモデルにて、5回シュート方向を予測した場合を例に scikit-learnのcohen_kappa_score関数を使ってweighted kappa loss を計算してみます。

weighted kappa loss 算出サンプルコード1

import numpy as np
from sklearn.metrics import cohen_kappa_score

# 正解シュート方向: [①左端、②中央左、③中央右、④右端 、①左端]
true = np.array([0, 1, 2, 3, 0])

# 推定シュート方向: [②中央左、②中央左、③中央右、④右端 、①左端]
pred = np.array([1, 1, 2, 3, 0])

epsilon = 1e-6

# weights='quadratic'オプションで重みを二乗で計算
kappa_score = cohen_kappa_score(true, pred, weights='quadratic')

print(f'kappa_score = {kappa_score}')
print(f'kappa_loss = {np.log(1 - kappa_score + epsilon)}')

出力結果1

kappa_score = 0.9180327868852459
kappa_loss = -2.5014237518136304

weighted kappa loss 算出サンプルコード2

import numpy as np
from sklearn.metrics import cohen_kappa_score

# 正解シュート方向: [①左端、②中央左、③中央右、④右端 、①左端]
true = np.array([0, 1, 2, 3, 0])

# 推定シュート方向: [②中央左、②中央左、③中央右、④右端 、①左端]
pred = np.array([3, 1, 2, 3, 0])

epsilon = 1e-6

# weights='quadratic'オプションで重みを二乗で計算
kappa_score = cohen_kappa_score(true, pred, weights='quadratic')

print(f'kappa_score = {kappa_score}')
print(f'kappa_loss = {np.log(1 - kappa_score + epsilon)}')

出力結果2

kappa_score = 0.4155844155844156
kappa_loss = -0.537141220973717

サンプルコード1、2の推定データはともに5本中4本のシュート方向を正しく分類できています。違いは1本のシュートを1クラス分だけ間違えたか、3クラス分間違えたかです。
weighted kappa loss はサンプルコード1(-2.501) < サンプルコード2(-0.537) となり、より大きく間違えているサンプルコード2の誤差を大きく算出できています。
weighted kappa loss は label distribution learning と同じく、順序をもつクラス分類タスクに有効な損失関数です。

おわりに

以上、順序をもつクラス分類タスクで使える手法 label distribution learning を紹介させていただきました。実際の業務では今回のように正解データの分布を変更する以外にも様々なパラメータをチューニングし、少しでも性能の良いモデルを作成できるよう繰り返し実験します。大変ですが試行錯誤が楽しくもあります。

オプティムでは1%の精度改善に情熱をそそぐエンジニアを募集しています。

ライセンス表記

記事内の画像はいらすとやさんの画像を使っています。ありがとうございます。

OPTiM TECH BLOG

順序をもつ分類タスクで使える手法「label distribution learning」をご紹介