はじめに
ICP（Iterative Closest Point）とは
- 点群の位置合わせ（Registration）
- ローカルとグローバル
基本のICP
色情報を使ったICP（Colored Point Cloud Registration）
- 目的関数
  - 概観
  - 色情報の項の詳細
- 目的関数の最適化
ICPを動かそう
まとめ

はじめに

こんにちは、R&Dユニットの葉山です。最近は測量アプリ Geo Scan の開発に取り組んでおり、その関係で点群を扱っております。今回は点群の位置合わせ（重ね合わせ）をご紹介させていただきます。基本的なICP（Iterative Closest Point）を説明したのち、その応用である色情報を活用したICP（Colored Point Cloud Registration）に関して解説を行います。

ICP（Iterative Closest Point）とは

点群の位置合わせ（Registration）

異なる位置から取得した（別々の座標系上で取得された）2つの点群に関して、その位置関係を推定して合成することは応用上重要になります。具体的には、三次元モデルの構築やロボティクス（空間認識等）などの場面で活躍します。

上図のように位置関係がわかっていない2つの点群を重ね合わせたい

点群の位置合わせ手法の中で代表的なものがICP（Iterative Closest Point）です。ICPでは、2つの点群を最適に重ね合わせることができる剛体変換（回転と並進）を反復計算によって求めます。*1

ローカルとグローバル

点群の位置合わせ手法にはローカル（Local Registration）とグローバル（Global Registration）の2種類があります。

ローカル手法は、初めから2つの点群同士がある程度重ね合わせられている（最適な重ね合わせ位置に近い）ことを前提としています。逆に、グローバル手法は初期位置に対する前提を必要としません。

本記事で紹介しているICPはローカルな位置合わせ手法になります。

基本のICP

まずは基本的なICPに関して概説します。

方針

source の点群（点の集合） $\mathbf{Q}$ を、target の点群 $\mathbf{P}$ に重ね合わせることを考えます。 $\mathbf{Q}$ の各点 $\mathbf{q}$ に対して変換行列 $\mathbf{T}$ を作用させ、その結果である $\mathbf{Tq}$ がどの程度 $\mathbf{P}$ に重なっているかを、 $\mathbf{T}$ に対する目的関数 $E(\mathbf{T})$ を設定して評価します。あとは、目的関数を最小化することで重ね合わせの変換行列である $\mathbf{T}$ を求めます。

最小化手法に何を使用するかは手法によって異なりますが、基本の ICP (point-to-point)の元論文*2では単純なニュートン法を使用して解くアプローチが取られています。本記事で紹介しますが、色付き ICP (Colored Point Cloud Registration) の場合はガウス・ニュートン法によって解くアプローチが取られています。*3

また、問題設定として $\mathbf{Q}$ と $\mathbf{P}$ のどの点同士が対応するかはわかっていませんので、 $E(\mathbf{T})$ の計算を行う上でも何らかの対応を与える必要があります。初期状態は各種手法で最近傍の点を求めそれを対応点とします。各繰り返しのステップでは変換後の $\mathbf{Tq}$ に対してまた最近傍の点 $\mathbf{p}$ と対応を取れば良いでしょう。最近傍点の探索はk近傍法やOctree等適切なアルゴリズムを使用することができます。

point-to-point

point-to-point と呼ばれる ICP は、名前の通り対応点同士の距離（の二乗和）を最小化するように目的関数を設定します。従って、目的関数 $E(\mathbf{T})$ は以下のようになります。

$\displaystyle E(\mathbf{T})={\sum}(\mathbf{p}-\mathbf{Tq})^2$

（以降でも省略していますが、 ${\sum}$ は $\mathbf{p}$ と $\mathbf{q}$ のペアに対して総和をとっているものとお考えください。）

point-to-plane

point-to-plane と呼ばれる ICP は、点と接平面に関して目的関数を設定します。「変換後の source の点 $\mathbf{Tq}$ から target の点 $\mathbf{p}$ へのベクトル」と「点 $\mathbf{p}$ の法線ベクトル」の内積が小さくなるように、目的関数 $E(\mathbf{T})$ は以下のようになります。

$\displaystyle E(\mathbf{T})={\sum}{( (\mathbf{p}-\mathbf{Tq}){\cdot}\mathbf{n_p})}^2$

なぜこの二つのベクトルの内積を取るかは以下の図を参照ください。

point-to-point より point-to-plane の方が収束までの時間は早くなる傾向にありますが、target の点群の法線が必要になります。情報がない場合は法線推定の手法を用いて事前に計算が必要になりますので、そこでの計算量と合わせてどちらの手法が優れるかは考慮が必要でしょう。*4

色情報を使ったICP（Colored Point Cloud Registration）

点群が位置情報の他に色情報を持っている場合、それらを活用することでより最適にかつ安定して点群の重ね合わせができる可能性があります。色情報を使ったICPはpoint-to-planeのICPの拡張版といえます。

目的関数

概観

目的関数は以下のように表されます。

$\displaystyle E(\mathbf{T})=(1-{\sigma})E_c(\mathbf{T})+{\sigma}E_g(\mathbf{T})$

ここで、 ${\sigma}$ はヒューリスティックな重み付けの定数であり、値は実験的に決定されます。*5

また、 $E_c(\mathbf{T})$ は色情報を使用した項であり、 $E_g(\mathbf{T})$ は位置情報を使用した項になります。各項の中身をそれぞれ見てみると、

$\displaystyle E_c(\mathbf{T})={\sum}{(C_p(\mathbf{f}(\mathbf{T}\mathbf{q}))-C(\mathbf{q}))}^2$

$\displaystyle E_g(\mathbf{T})={\sum}{( (\mathbf{p}-\mathbf{Tq}){\cdot}\mathbf{n_p})}^2$

となっており、 $E_g(\mathbf{T})$ はそのままpoint-to-planeの場合の目的関数と一致します。従って、 ${\sigma}=1$ の場合はpoint-to-planeのICPと一致することがわかります。

後の最適化の説明で使用するので、ここでは $\sum$ の二乗和の中身をそれぞれ以下のように置いておきます。後の説明のために $\mathbf{s(q, T)} = \mathbf{Tq}$ と関数を置いていることに注意ください。

$\displaystyle r_c(\mathbf{T})=C_p(\mathbf{f}(\mathbf{s(q, T)}))-C(\mathbf{q})$

$\displaystyle r_g(\mathbf{T})=(\mathbf{p}-\mathbf{s(q, T)}){\cdot}\mathbf{n_p}$

色情報の項の詳細

さて、次は色情報を使った項を細かく見ていきます。

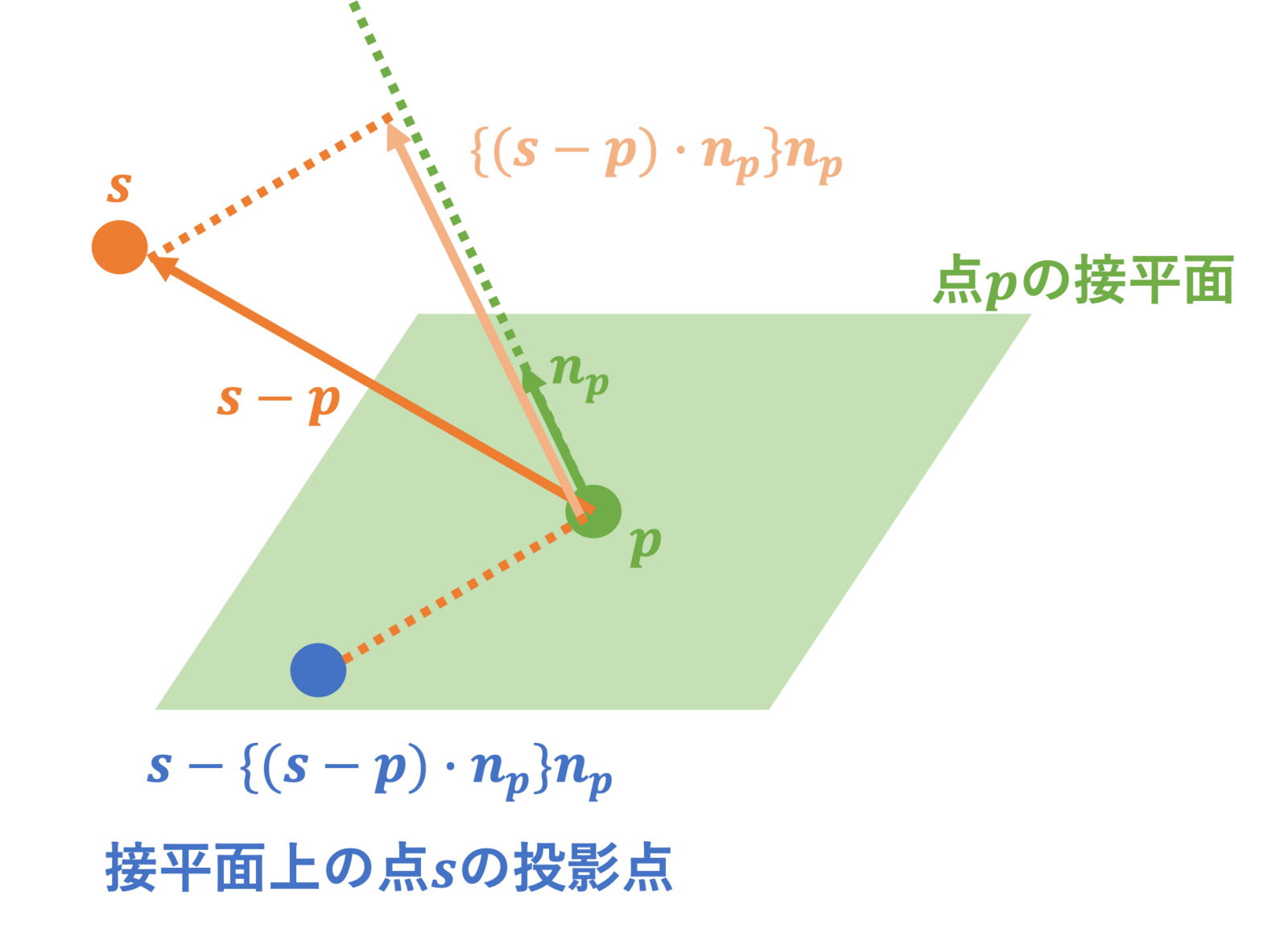
まず、関数 $\mathbf{f}(\mathbf{s})$ は、ある3次元空間上の点 $\mathbf{s}$ に対して、点 $\mathbf{p}$ の接平面に対する投影点を得る関数です。定義は以下のようになります。

$\displaystyle \mathbf{f}(\mathbf{s})=\mathbf{s}-\{(\mathbf{s}-\mathbf{p}){\cdot}\mathbf{n_p}\}\mathbf{n_p}$

この関数に関しては、以下の図に示すように点 $\mathbf{s}$ を接平面に対して投影していることがわかります。

次に、関数 $C(\mathbf{q})$ は、点群中の点 $\mathbf{q}$ に関する色情報を出力する関数です。

最後に、関数 $C_p(\mathbf{u})$ は接平面上で点 $\mathbf{p}$ から $\mathbf{u}$ ずれた位置（つまり、 $\mathbf{u}{\cdot}\mathbf{n_p}=0$ の条件がある）の色を返す関数ですが、近似によって以下のように表すことができます。

$\displaystyle C_p(\mathbf{u}){\approx}C(\mathbf{p})+\mathbf{d_p}{\cdot}\mathbf{u}$

連続関数として考えている $C_p(\mathbf{u})$ に関して、点 $\mathbf{p}$ まわりの展開を一階微分で切った形になります。 $\mathbf{d_p}$ は $C_p(\mathbf{u})$ のgradientであり、実際には点 $\mathbf{p}$ の近傍点を使って最小二乗法によって計算されます。

以上より、色情報を使った項 $E_c(\mathbf{T})$ は、「点 $\mathbf{p}$ 」と「点 $\mathbf{Tq}$ を接平面に投影した点」の「色情報ベクトルの差（の2乗）」の総和であることがわかります。

目的関数の最適化

色情報を使った ICP の元論文で紹介されている最適化のプロセスを、ここでは簡単にご紹介させていただきます。 $E(\mathbf{T})$ をガウス・ニュートン法で最適化する方式です。

ガウス・ニュートン法の詳細はここでは省きますが、ヤコビアン $\mathbf{J}$ と残差（ここでは $\mathbf{p}$ と $\mathbf{Tq}$ の差） $\mathbf{r}$ があるとき、

$\displaystyle \mathbf{J}^T \mathbf{J}\Delta\mathbf{\lambda_k} = \mathbf{J}^T\mathbf{r}$

となるような $\Delta\mathbf{\lambda_k}$ が分かれば、次のステップの値 $\mathbf{\lambda_{k+1}}$ は以下の式で求めることができます。

$\displaystyle \mathbf{\lambda_{k+1}} =\mathbf{\lambda_k} + \Delta\mathbf{\lambda_k}$

さて、色情報を使った ICP に関して、あるステップ k+1 の変換行列 $\mathbf{T_{k+1}}$ は、 $\mathbf{T_k}$ を用いて以下のように線形に近似します。 $\mathbf{T_k}$ から少しだけ回転 & 並行移動したイメージかと思われます。

$\displaystyle \mathbf{T_{k+1}} \approx \left( \begin{array}{rr} 1 & -\gamma & \beta & a \\ \gamma & 1 & -\alpha & b \\ -\beta & \alpha & 1 & c \\ 0 & 0 & 0 & 1 \\ \end{array} \right) \mathbf{T_k}$

ここで $\mathbf{\xi} = (\alpha, \beta, \gamma, a, b, c)$ という6要素のベクトルを置くと、ヤコビアンと残差を用いて以下の式が成り立ちます。

$\displaystyle \mathbf{J}^T \mathbf{J}\mathbf{\xi} = \mathbf{J}^T\mathbf{r}$

この線型方程式を解いて $\mathbf{\xi}$ を求め、次のステップの変換行列の値を求めます。

残差とヤコビアンを位置情報の項と色情報の項に分けて考えると、以下のようになります。

$\displaystyle \mathbf{r} = [\sqrt{1-{\sigma}}\mathbf{r}_c;\sqrt{\sigma}\mathbf{r}_g$ ]

$\displaystyle \mathbf{r}_c = r_c(\mathbf{T})|_{\mathbf{T}=\mathbf{T_k}}$

$\displaystyle \mathbf{r}_g = r_g(\mathbf{T})|_{\mathbf{T}=\mathbf{T_k}}$

$\displaystyle \mathbf{J} = [\sqrt{1-{\sigma}}\mathbf{J}_c;\sqrt{\sigma}\mathbf{J}_g$ ]

$\displaystyle \mathbf{J}_c = \nabla r_c(\mathbf{T})|_{\mathbf{T}=\mathbf{T_k}}$

$\displaystyle \mathbf{J}_g = \nabla r_g(\mathbf{T})|_{\mathbf{T}=\mathbf{T_k}}$

ヤコビアンに出てくる $\nabla r_c$ と $\nabla r_g$ ですが、微分の chain rule を用いて以下のように変形できます。

$\displaystyle \nabla r_c(\mathbf{T}) = \frac{\partial}{\partial\mathbf{\xi}}(C_p \circ \mathbf{f} \circ \mathbf{s}) = \nabla C_p(\mathbf{f})\mathbf{J_f}(\mathbf{s})\mathbf{J_s}(\mathbf{\xi})$

$\displaystyle \nabla r_g(\mathbf{T}) = \mathbf{n_p}^T\mathbf{J_s}(\mathbf{\xi})$

$\nabla C_p$ は $C_p$ の gradient なので、色情報の項で出てきた $\mathbf{d_p}$ ですね！ $\mathbf{J_f}$ は $\mathbf{f(s)}$ に関するヤコビアン、 $\mathbf{J_s}$ は $\mathbf{s(\mathbf{\xi})}$ に関するヤコビアンであり、それぞれの式から導出が可能です。

ICPを動かそう

本記事で解説している ICP は、 Open3D を用いて簡単に動かすことができます。興味がある方はぜひお試しください。

www.open3d.org

参考までに、 point-to-plane を動かす場合の Python スクリプトは以下のようになります。点群は X, Y, Z, R, G, B のような順序でスペース区切りで格納しておけば読み込めます（RGBは[0-1]に正規化が必要）。入出力の詳細は Open3D のリファレンスをご確認ください。以下のスクリプトを見るとわかる通り、 point-to-plane の場合 target の点群に対して（法線の情報がないなら）法線推定が必要になります。

import argparse
from pathlib import Path

import open3d as o3d

def parse_args():
    parser = argparse.ArgumentParser()

    # 各パラメータは点群に応じて調整
    parser.add_argument('--max_correspondence_distance', type=float, default=0.02)
    parser.add_argument('--max_iteration', type=int, default=500)
    parser.add_argument('--estimate_normals_max_nn', type=int, default=30)
    parser.add_argument('--estimate_normals_radius', type=float, default=0.1)

    parser.add_argument('--pcd_source', type=Path)
    parser.add_argument('--pcd_target', type=Path)

    return parser.parse_args()

def main(args):
    pcd_source = o3d.io.read_point_cloud(str(args.pcd_source))
    pcd_target = o3d.io.read_point_cloud(str(args.pcd_target))

    assert pcd_source.has_points()
    assert pcd_source.has_colors()
    assert pcd_source.dimension() == 3
    assert pcd_target.has_points()
    assert pcd_target.has_colors()
    assert pcd_target.dimension() == 3

    # 事前に点群の重なり具合の評価値を確認しておくと、ICP の有効性が確認しやすい
    evaluation = o3d.pipelines.registration.evaluate_registration(
        source = pcd_source,
        target = pcd_target,
        max_correspondence_distance = args.max_correspondence_distance)

    # target の点群の法線推定
    pcd_target.estimate_normals(
        search_param=o3d.geometry.KDTreeSearchParamHybrid(
            radius=args.estimate_normals_radius,
            max_nn=args.estimate_normals_max_nn
        )
    )

    # point-to-plane ICP を適用
    reg = o3d.pipelines.registration.registration_icp(
        source = pcd_source,
        target = pcd_target,
        max_correspondence_distance = args.max_correspondence_distance,
        estimation_method = o3d.pipelines.registration.TransformationEstimationPointToPlane(),
        criteria = o3d.pipelines.registration.ICPConvergenceCriteria(max_iteration=args.max_iteration)
    )

    # reg.transformation が結果の変換行列
    pcd_source.transform(reg.transformation)
    o3d.io.write_point_cloud(str(args.pcd_source.parent / 'icp.ply'), pcd_source)

if __name__ == '__main__':
    main(parse_args())

まとめ

本記事では基本のICPから、色情報を使ったICPまでを概説しました。色情報を使ったICPも、数式を紐解いていけば考え方は非常に単純であることがわかります。色情報を持っている点群を扱う場合は、ケースに応じてColored Point Cloud Registrationもぜひ活用していきたいところです。

オプティムではAI・IoT技術によりビジネス課題・社会的課題の解決を目指しています。ぜひ以下の採用情報もご覧ください。

www.optim.co.jp

*1:お察しの通り非剛体（Non-rigid）な手法も存在します。本記事で紹介するICPはrigidな手法になります。

*2:Paul J. Besl and Neil D. McKay, A Method for Registration of 3D Shapes, PAMI, 1992.

*3:J. Park, Q.-Y. Zhou, and V. Koltun, Colored Point Cloud Registration Revisited, ICCV, 2017.

*4:http://www.open3d.org/docs/release/tutorial/pipelines/icp_registration.html

*5:Open3Dでのデフォルト値は0.968のようです https://github.com/isl-org/Open3D/blob/aebdb9a4396808edece4c24156e0231dc47a5edd/cpp/open3d/pipelines/registration/ColoredICP.h#L74

OPTiM TECH BLOG

点群の重ね合わせに色情報も活用しよう！（Colored Point Cloud Registration の解説）