OPTiM TECH BLOG Advent Calendar 2020 12/8 の記事です。
お久しぶりです。R&Dの加藤です。最近買った大きな買い物はDAHONのK3です。
購入したのは8月末ですが、11月に入るまでスタンドが手に入らなかったです。現状の不満点は空気が入れにくいという事だけですね。輪行するには最適な自転車です。
去年執筆したこの記事はいまだに定期的にアクセスがあって嬉しいですね。まだ読んでない方は是非こちらも読んでみてください。
今回の記事はこれの補足に加え、コードを加えた実践的な内容になります。
記事執筆のモチベーションとしては、「最近PyCMというライブラリを使い始めたら思いのほか便利だったので伝えたい」という事なんですが、なかなかボリュームのある記事になってしまいました。忙しい人は必要な章だけかいつまんで読んでください。
PyCMとは
本家のサイトはこちらになります。
PyCMとはなんぞや?という事で、本家から一部引用してみます。
PyCM is a multi-class confusion matrix library written in Python that supports both input data vectors and direct matrix, and a proper tool for post-classification model evaluation that supports most classes and overall statistics parameters. PyCM
マルチクラスの混同行列に対応し、多くの統計パラメータ(評価指標)を網羅しているとあります。
たしかにバージョン3.0時点でBasic Parameter(9個)、Class statistics(55個)、Overall statistics(66個)に加えて標準出力関数や保存関数まで備えています。
どんな評価指標があるかはDocumentに丁寧に書かれていますが、PyCMを手っ取り早く試すにはExampleから読むのがオススメです。
さて、上述したように100個を超える評価指標が用意されており、私自身「多すぎて実際にどれを使えばいいのかわからない」となりました。
特に異常検知系のセグメンテーションではTrue Negative(TN)が多くなりすぎる傾向があるので、TNを使用しない評価指標が欲しかったのです。
という事で、私がセグメンテーションの評価に適切な評価指標をいくつか選定しましたので、それを紹介していきます。 その前に、画像分類でPyCMのチュートリアルをやってみましょう。
PyTorchのexampleを例として、画像分類にPyCMを適用
PyTorchのサンプルプログラムを改変してPyCMを使ってみましょう。
サンプルプログラムは何でもいいので、とりあえず馴染みのあるMNISTを使います。
実装(PyTorchのexample/mnistを改造)
まずは素直にPyCMでマルチクラスの混同行列を出力してみましょう。お題はPyTorchのexampleにあるMNISTです。
学習完了時に、テストデータをPyCMによって可視化することを目的とします。main関数のfor文以降に以下を記載しましょう。
for epoch in range(1, args.epochs + 1): train(args, model, device, train_loader, optimizer, epoch) test(model, device, test_loader) scheduler.step() confusion_mat(model, device, test_loader) # 追加
comfusion_matの実装はこんな感じです。
def plot_cm(cm, normalize=False, title='Confusion matrix', annot=False, cmap='YlGnBu'): import pandas as pd import seaborn as sns data = cm.matrix if normalize: title += '(Normalized)' data = cm.normalized_matrix df = pd.DataFrame(data).T.fillna(0) ax = sns.heatmap(df, annot=annot, cmap=cmap, fmt='d') ax.set_title(title) ax.set(xlabel='Predict', ylabel='Actual') def confusion_mat(model, device, test_loader): import matplotlib.pyplot as plt from pycm import ConfusionMatrix model.eval() out = list() tgt = list() with torch.no_grad(): for data, target in test_loader: data, target = data.to(device), target.to(device) pred = model(data).argmax(dim=1, keepdim=True) # ConfusionMatrix用にデータを成形 out.extend(pred.cpu().numpy().reshape(-1).tolist()) tgt.extend(target.cpu().numpy().reshape(-1).tolist()) cm = ConfusionMatrix(actual_vector=tgt, predict_vector=out) # 混同行列の標準出力 cm.print_matrix() # confusion_mat.objの保存 cm.save_obj('confusion_mat') # 混同行列をpandasとseabornで可視化 plt.figure() plot_cm(cm, annot=True) plt.savefig('confusion_mat.png', bbox_inches='tight') # confusion_mat.objは以下のようにして読み込んで再利用できるので便利 cm_load = ConfusionMatrix(file=open('confusion_mat.obj', 'r')) cm_load.print_matrix(sparse=True)
plot_cmに関しては以下(PyCMのExample 7)を参考にしています。
MNISTを動かしてみる
これを実行すると、以下のように処理が完了します(各自で足りないライブラリをpip installしてください)。
$ python ./main.py --epoch 3 Train Epoch: 1 [0/60000 (0%)] Loss: 2.325871 Train Epoch: 1 [640/60000 (1%)] Loss: 1.399990 : Train Epoch: 1 [59520/60000 (99%)] Loss: 0.124199 Test set: Average loss: 0.0487, Accuracy: 9849/10000 (98%) Train Epoch: 2 [0/60000 (0%)] Loss: 0.030074 Train Epoch: 2 [640/60000 (1%)] Loss: 0.158760 : Train Epoch: 2 [59520/60000 (99%)] Loss: 0.121354 Test set: Average loss: 0.0401, Accuracy: 9858/10000 (99%) Train Epoch: 3 [0/60000 (0%)] Loss: 0.025359 Train Epoch: 3 [640/60000 (1%)] Loss: 0.175206 : Train Epoch: 3 [59520/60000 (99%)] Loss: 0.010523 Test set: Average loss: 0.0326, Accuracy: 9891/10000 (99%) Predict 0 1 2 3 4 5 6 7 8 9 Actual 0 976 0 0 0 0 1 1 1 1 0 1 0 1131 1 1 0 0 2 0 0 0 2 2 3 1021 0 0 0 0 5 1 0 3 0 0 3 1002 0 4 0 0 1 0 4 0 0 1 0 968 0 3 0 2 8 5 2 0 0 5 0 882 3 0 0 0 6 5 1 0 0 1 3 946 0 2 0 7 0 2 7 1 0 0 0 1014 1 3 8 3 1 1 1 2 0 2 1 959 4 9 2 2 0 0 3 3 0 3 4 992 hoge\lib\site-packages\pycm\pycm_obj.py:115: RuntimeWarning: The confusion matrix is a high dimension matrix and won't be demonstrated properly. If confusion matrix has too many zeros (sparse matrix) you can set `sparse` flag to True in printing functions otherwise by using save_csv method to save the confusion matrix in csv format you'll have better demonstration. warn(CLASS_NUMBER_WARNING, RuntimeWarning) Predict 0 1 2 3 4 5 6 7 8 9 Actual 0 976 0 0 0 0 1 1 1 1 0 1 0 1131 1 1 0 0 2 0 0 0 2 2 3 1021 0 0 0 0 5 1 0 3 0 0 3 1002 0 4 0 0 1 0 4 0 0 1 0 968 0 3 0 2 8 5 2 0 0 5 0 882 3 0 0 0 6 5 1 0 0 1 3 946 0 2 0 7 0 2 7 1 0 0 0 1014 1 3 8 3 1 1 1 2 0 2 1 959 4 9 2 2 0 0 3 3 0 3 4 992 hoge\lib\site-packages\pycm\pycm_obj.py:115: RuntimeWarning: The confusion matrix is a high dimension matrix and won't be demonstrated properly. If confusion matrix has too many zeros (sparse matrix) you can set `sparse` flag to True in printing functions otherwise by using save_csv method to save the confusion matrix in csv format you'll have better demonstration. warn(CLASS_NUMBER_WARNING, RuntimeWarning)
(このWarning消したかったんですけど、sparce=Trueでも変わらなかったので良くわからんです)
学習が無事に完了したと思います。PredictとActualの表が2回出力されていますが、間違いではありません。 PyCMでは混同行列を読み書きする機能があり、それを試しているためです。
PyCMによるMNISTの学習結果の可視化
実行完了するとexampleディレクトリ直下にconfusion_mat.objとconfusion_mat.pngができていると思います。画像の方はこんな感じですね。オシャレ。
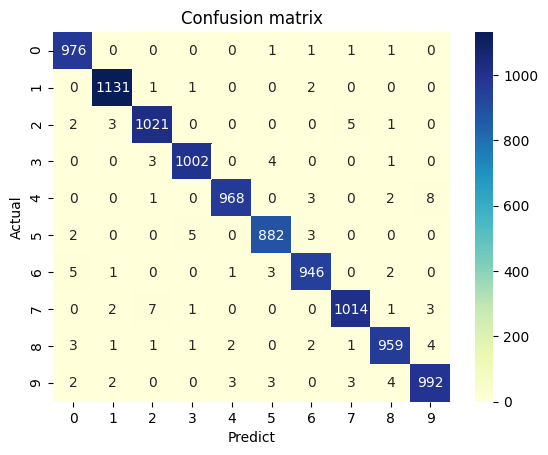
confusion_mat.objは出力しておくと、それを再読み込みするだけで色々な指標を再計算できます。
再度推論させる必要がないので、CPU環境でも簡単に確認できたりメリットが多いので、objだけでも出力しておくといいです。
ちなみにconfusion_mat.objの中身はこのようになっています。
{"Actual-Vector": [6, 3, 6, ..., 9, 1, 7], "Predict-Vector": [6, 3, 6, ..., 9, 1, 7], "Matrix": [[0, [[0, 976], [1, 0], [2, 0], [3, 0], [4, 0], [5, 1], [6, 1], [7, 1], [8, 1], [9, 0]]], [1, [[0, 0], [1, 1131], [2, 1], [3, 1], [4, 0], [5, 0], [6, 2], [7, 0], [8, 0], [9, 0]]], ...]], "Digit": 5, "Sample-Weight": null, "Transpose": false}
補足(ラベルの適用)
MNISTだからデフォルトのラベル(0-9)でいいですが、変えたい場合はrelabelを使ってください。
U-Netを利用したセグメンテーションにPyCMを適用
画像分類のチュートリアルで、PyCMの使い方はなんとなくわかったと思います。セグメンテーションも結局は各ピクセルレベルの画像分類なので、同じようにPyCMが使えるのでは?ということで今度はセグメンテーションにPyCMを適用します。
実装(MNISTベースにU-Netとデータセット生成&読込み部分の追加)
コードの全貌はGitHubにアップロードしました。細かい所は好みで修正していますが、基本的には先ほどのMNISTベースの構成になっています。
気軽にスターを押してもらえると泣いて喜びます。
以下では実装にあたってMNISTベースから大きく変わった部分のみ記載していきます。
U-Netモデルの呼び出し
セグメンテーションといえばやはり個人的にはU-Netが良いですね。医療分野の異常検知系で良く使われるネットワークモデルです。派生にR2U-NetやAttention U-Net、U2-Netがあります。
様々な人がU-Net系のネットワークモデルをGitHubで公開していますが今回は簡単にtorch.hubから呼び出してみます。
今回は全く新しいデータセットを使って学習させるので、pretrained=Falseにしています。main関数内で以下のように記述します。
model = torch.hub.load(
'mateuszbuda/brain-segmentation-pytorch', 'unet',
in_channels=3, out_channels=1, init_features=32, pretrained=False
).to(device)
データセット生成&読込み
セグメンテーションのデータセットで手ごろなものがなかったので今回は自作しています。 以下のようなデータセットを作成するコードを用意しました。

上段が入力画像で、下段が正解画像です。
入力画像はランダムに配置された円や矩形の図形上に文字を並べたもので、正解画像は文字だけを抽出したものになります。ランダムに画像を生成しているだけなので、1,000枚でも10,000,000枚でも好きなだけ画像を生成できて、ストレージも不要なデータセットです(ただし画像生成にそれなりの計算コストがかかります)。
データセットの作成は以下のようにOpenCVを使っています。ImageGeneratorについては記載を省略しますが、自作の簡易画像処理ラッパーです。
from torch.utils.data import Dataset from torchvision import transforms def read_imgs(ig): # 文字を追加 img = ig.add_str().img # 画像を二値化して正解画像を作成 target_img = ig.to_binary(10).img # 背景画像生成のためにリセット ig.reset() # 背景を追加して、文字を入れる分を除去する bg = ig.add_pattern().bitwise_and(target_img).img # 背景画像と文字画像で入出力画像を生成 input_img = img + bg # 次の処理のためにリセット ig.reset() return input_img, target_img class MyDataset(Dataset): def __init__(self, seed, resize=128, img_num=100): self.ig = ImgGenerator(400, 400, seed) self.img_num = img_num # set transforms self.transform_x = transforms.Compose([ transforms.Resize(resize), transforms.ToTensor(), ]) self.transform_y = transforms.Compose([ transforms.Resize(resize), transforms.ToTensor() ]) def __getitem__(self, idx): # 画像生成呼び出し x, y = read_imgs(self.ig) # transformsがPIL形式じゃないと使えないので、transformする前に変換 x = self.transform_x(Image.fromarray(x)) y = self.transform_y(Image.fromarray(y)) return x, y def __len__(self): return self.img_num
これをmain関数内で以下のようにして呼ぶことで、MNIST以外のデータセットが学習できます。
train_loader = DataLoader(MyDataset(100, img_num=10000), **train_kwargs) test_loader = DataLoader(MyDataset(101), **test_kwargs)
乱数生成用のseedは100と101にしていますが、なんでもいいです。ただ、trainとtestで別の数字にした方が良いと思います。
PyCMまわりの実装
confusion_matはMNISTの時とは異なり、今回は画像1枚ごとにピクセルレベルでTrue Positive(TP)、False Positive(FP)、False Negative(FN)を判定する必要があるので、その分コードが増えています。
PyCMではTP、FP、FNすべて自動で計算してくれますが、画像の可視化パートではOpenCVの論理演算で計算しています。
def confusion_mat(model, device, test_loader, fmt='3.1%'): model.eval() with torch.no_grad(): print('TPR PPV G J F1 AUPR') # バッチサイズ毎に画像を読み込み for data, target in test_loader: tgt = _to_imgs(target) src = _to_imgs(data, binary=False) data, target = data.to(device), target.to(device) out = _to_imgs(model(data).cpu()) # 画像一枚ずつ処理 for x, y, z in zip(tgt, out, src): # 画像の可視化に必要な処理 b = np.zeros_like(x) tp = cv2.bitwise_and(x, y) ntp = cv2.bitwise_not(tp) fp = cv2.bitwise_and(y, ntp) fn = cv2.bitwise_and(x, ntp) dst = cv2.merge([b, tp + fp, fn + fp]) cv2.imshow('test', cv2.resize(np.vstack([z, dst]), (300, 600))) if cv2.waitKey(20) == ord('q'): return 0 # PyCM用の処理 x = x.reshape(-1) // 255 y = y.reshape(-1) // 255 cm = ConfusionMatrix(actual_vector=x, predict_vector=y) print( f'{cm.TPR[1]:{fmt}}, {cm.PPV[1]:{fmt}}, {cm.G[1]:{fmt}}, ' + f'{cm.J[1]:{fmt}}, {cm.F1[1]:{fmt}}, {cm.AUPR[1]:{fmt}}' )
上記までのコードを踏まえると、main関数内のデータセット読込みから学習、PyCM実行までは以下のようになります。
# データローダー定義 train_loader = DataLoader(MyDataset(100, img_num=10000), **train_kwargs) test_loader = DataLoader(MyDataset(101), **test_kwargs) # ネットワークモデル定義 model = torch.hub.load( 'mateuszbuda/brain-segmentation-pytorch', 'unet', in_channels=3, out_channels=1, init_features=32, pretrained=False ).to(device) # 学習させる場合 if args.weight is None: optimizer = optim.Adadelta(model.parameters(), lr=args.lr) scheduler = StepLR(optimizer, step_size=1, gamma=args.gamma) for epoch in range(1, args.epochs + 1): train(args, model, device, train_loader, optimizer, epoch) test(model, device, test_loader) scheduler.step() torch.save(model.state_dict(), 'unet_weight.pt') # 学習済みの重みを利用する場合 else: state = torch.load( args.weight.as_posix(), map_location=lambda storage, loc: storage ) model.load_state_dict(state) # PyCMで混同行列を計算 confusion_mat(model, device, test_loader)
PyCMによるセグメンテーションの可視化
これを実行すると、以下のように処理が完了します(各自で足りないライブラリをpip installしてください)。
unet_weight.ptは学習終了時にディレクトリ直下に保存されるネットワークモデルの重みパラメータです。
初めて実行する際は存在しないので、引数を除外して実行してください(学習がはじまります)。
python ./main.py --wei ./unet_weight.pt Using cache found in hoge/.cache/torch/hub/mateuszbuda_brain-segmentation-pytorch_master TPR PPV G J F1 AUPR 64.4%, 94.9%, 78.1%, 62.2%, 76.7%, 79.6% 70.7%, 86.5%, 78.2%, 63.6%, 77.8%, 78.6% 38.3%, 65.5%, 50.1%, 31.9%, 48.3%, 51.9% 47.5%, 88.2%, 64.7%, 44.7%, 61.7%, 67.9% 65.8%, 90.7%, 77.3%, 61.7%, 76.3%, 78.3% 43.9%, 83.9%, 60.7%, 40.5%, 57.6%, 63.9% 44.5%, 79.1%, 59.3%, 39.8%, 57.0%, 61.8% 62.8%, 72.0%, 67.3%, 50.5%, 67.1%, 67.4% 73.0%, 83.3%, 78.0%, 63.7%, 77.8%, 78.2% :
実行すると、以下のような画像が表示されます。上段が入力画像で、下段は推論画像と正解画像を比較した結果(分析結果)になります。
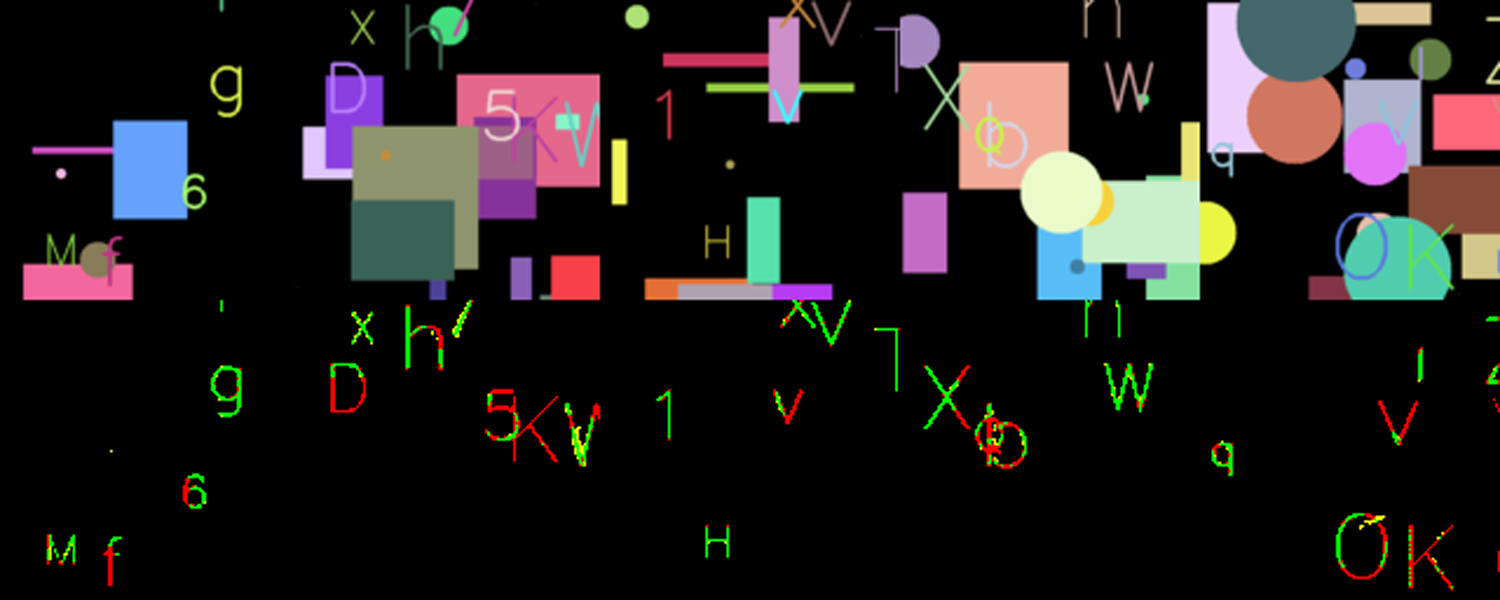
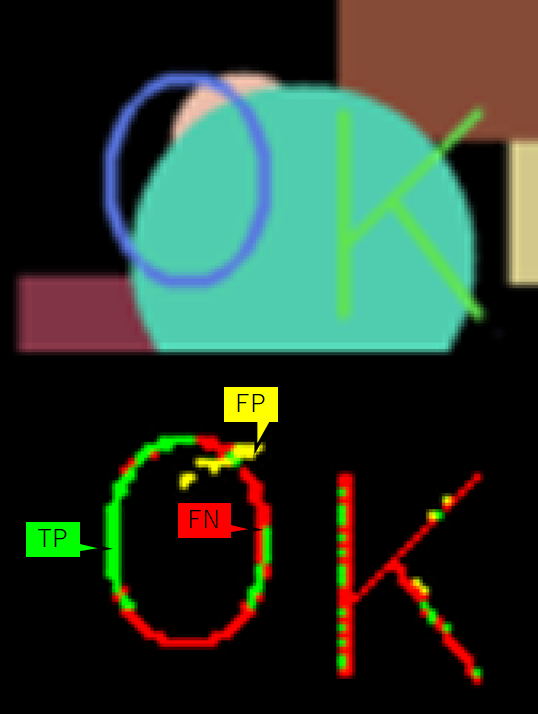
下段の分析結果の緑、黄、赤はそれぞれ以下の図のようにTP、FP、FNに対応しています。

先ほどの入力画像と分析結果を拡大してみました。背景色と文字色が近いと上手く検出されない(赤い)場合が多いように見えますね。
この改善方法を議論しだすと終わらなくなるので割愛します。
さて、本題の評価指標についてですがTPR、PPV、G、J、F1、AUPRという評価指標を今回選定しています。
異常検知系のセグメンテーションではTrue Negative(TN)が多くなりすぎる傾向があるので、「TNを使用しない評価指標であること」が重要です。
評価指標の紹介
以下では各評価指標の解説をしていきます(一部去年のブログから引用しています)。
Positive predictive value(PPV)
PPVは適合率(Precision)と呼ばれることもあります。
PPVはPositiveを確認する指標になります。数式にFNが含まれていないので、いくら見逃していようが、PositiveがすべてTrue(FP=0)ならばPPVは100%になります。つまり誤検知にどれだけ強いかを測定する指標ともいえますね。
True Positive Rate(TPR)
TPRは感度(Sensitivity)や再現率(Recall)と呼ばれることもあります。
TPRはPPVと異なり、Negativeを確認する指標になります。数式にFPが含まれていないので、いくら誤検知していようが、FNが0ならばTPRは100%になります。つまり見逃しにどれだけ強いかを測定する指標ともいえます。
農業でも医療でも、誤検知は運用でカバーしやすいですが見逃しはそうもいかないので、PPVよりもTPRを重視する場合がほとんどです。
F1
F1はPPVとTPRの調和平均になります。これを数式で表現すると以下の通りです。
PPV(誤検知NG)とTPR(見逃しNG)はトレードオフの関係ですが、どっちも欲しいというワガママな指標がF1です。 別名Dice係数と呼ばれています。
Jaccard index(J)
Jは数式で表現すると以下の通りです。
オーバーラップ率やIntersection over Union(IoU)とも呼ばれています。
G-measure(G)
Gは数式で表現すると以下の通りです。
Jと似ていますが、分母が若干異なりますね。
Area under the PR curve(AUPR)
Gに似ているますが、こちら根号ではなく平均です。
だんだん式が複雑になってきました。複雑な方が網羅性のあるいい指標と思いがちですがどうなんでしょうか?もう少し比較してみましょう。
F1、J、G、AUPRの比較
PPVとTPRを組み合わせた指標が4種類出てきました。果たしてそれぞれどうやって使い分けたらいいのか理解するべくそれぞれの特性を可視化していきます。
変数が、TP、FP、FNと3種類あると比較が難しいので変数を一本化します。
FP=FN=X とした場合
簡単のために、FPとFNを共にXと置くと、以下のようになります。
AUPRだけ分子にA(=X/TP)が登場しました。覚えておきましょう。
FP=X、FN=5Xとした場合
今度はFP=X、FN=5X(FP+FN=6X)とバランスが悪い場合を検証します。
基本的にはFP=FN=Xの時と変わらなそうですね。
ただし、AUPRの分子がAから6Aになっています。AUPRだけ分子が大きくなっている気がしますが大丈夫でしょうか?
グラフによる比較
先ほど導出した式を使って、以下のようにグラフを作成してみました。
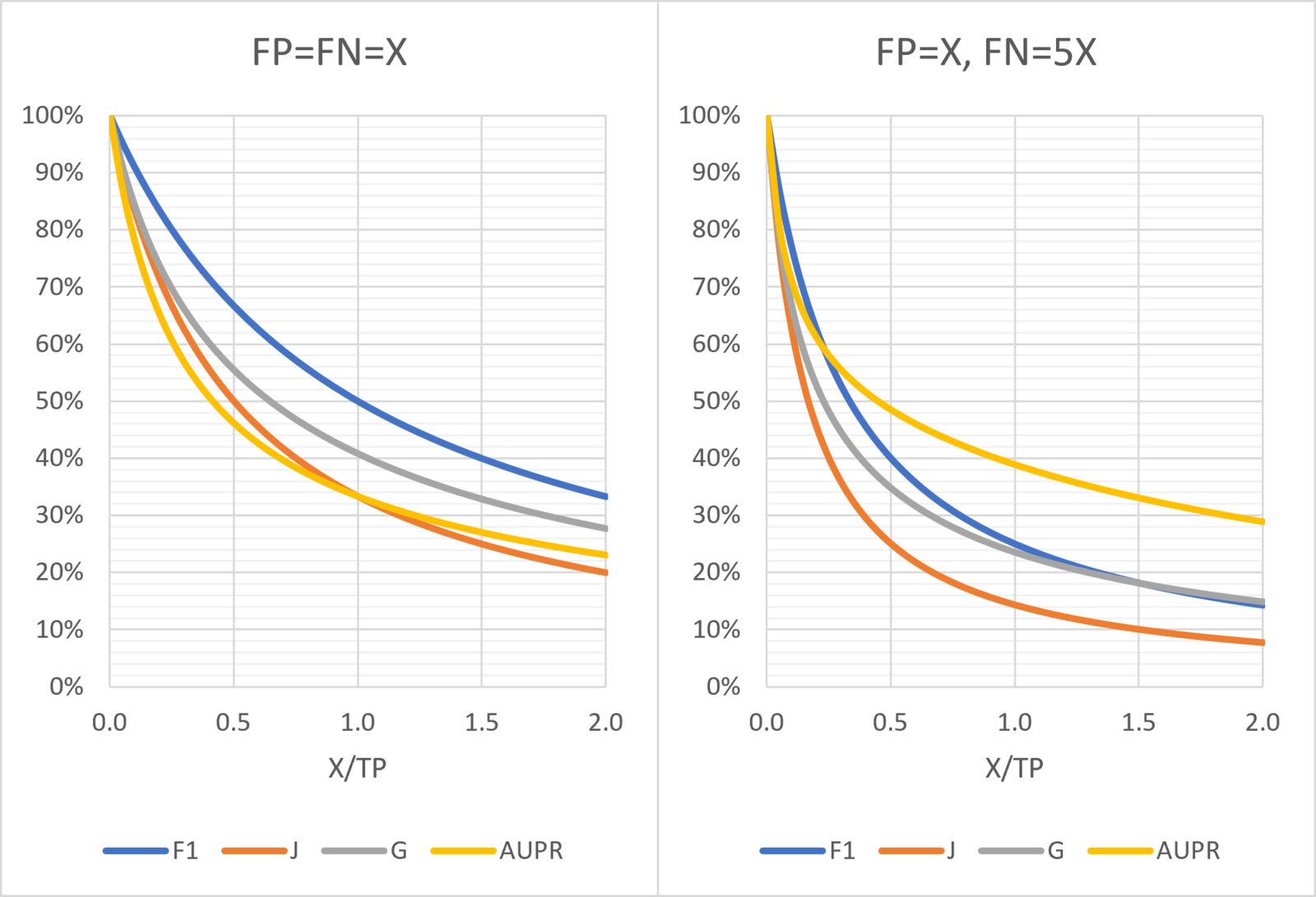
- 基本的にはJが一番指標として低い値(前回ブログと同様の結果)
- AUPRはFPとFNのバランスが悪い時にかなり高くなる傾向(良くない)
- GはX/TP<0.1の時にJに近い結果になり、その後F1に近づく
という事がわかります。AUPRが極端に良くなるのは、やはり分子の6Aが効いているような気がします。
個人的にはGが比較的なだらかな曲線になっているのでオススメですが、これもAUPRほどではないにしろFPとFNのバランス悪い時にF1を超える場合があるので注意が必要です。
最後に
いかがだったでしょうか?PyCMを使うことで、画像分類タスクでもセグメンテーションタスクでも簡単に可視化できるようになりました。少ないコードで実現できるので是非みなさんも試してみてください。
また、セグメンテーションの指標としてはAUPRはあまりオススメできず、Gが一番バランスが良いのではないかと思います。
OPTiMでは農業医療に限らず、土木やサービス業など幅広くITを推進しているので、少子高齢化や人手不足をダイレクトに解決したいチャレンジャーなエンジニアのみなさんを募集しています!
(最近は新型コロナウイルスのこともあり、活動できてないですが)一緒に皇居を走ったり、マラソン大会に参加してくれたりするマルチなエンジニアも募集しています!